样本选择模型——Heckman两步法
样本选择模型——Heckman两步法
1. 内生性来源——样本选择偏差
在内生性的问题中，而对于选择导致结果估计不一致的偏差可以分为两种情况：（1）样本自选择偏差；（2）样本选择偏差。导致偏差的关键的在于两者非随机的选择机制是不同的：非随机选择机制的不同是两者最大的区别，体现在具体回归方程中就是，前者指的是由于哑元解释变量
样本选择偏差：指的是样本抽取的时候选择不随机所导致的偏差。因为当我们在样本抽样的时候，没有做到样本抽取的随机性，仅仅支队某部分的人群进行调查，使得这部分群体于其他群体在某些方面的特征差异很大而导致最终不随机样本回归得不到稳健可信的结论。可以这么理解为幸存者偏差，举一个例子：
我们想要调研感染omicron这种病毒后的重症率是多大？在网络上发布一个问卷进行调研，发现大部分人感染了omicron后几乎都是较轻的症状，得出结果是：omicron的重症率很低
但是这个例子中关于调研样本的抽取是存在问题，感染了omicron的人如果有重症大部分都是老人或者小孩，他们都不具有上网填写调查问卷的条件，另外当处于重症的情况下也不会有心思去填问卷（好好养病吧，别看手机了），所以最终能够填写调查问卷的都是些身强力壮的年轻人或者是感染后症状较轻的人。体现在我们所采集的数据集中就是数据集中仅仅只覆盖了某部分特定的人群样本（假设轻症可以填问卷，重症病的填不了），就会导致其他群体的数据缺失，在这种情况下进行回归，都将会直接忽视掉其他群体的样本信息。实质上，样本选择偏差说的就是参与回归的样本不能代表总体从而产生估计偏误的问题。或许就是我们常说的幸存者偏差。
2. Heckman两步法基本原理
对于这种造成偏误的情况，我们可以利用赫克曼矫正法（Heckman Correction，又称两阶段方法）来解决由于样本选择偏差造成的内生性问题，通过两阶段步骤来完成：
第一步骤：建立一个 Probit 模型估计是否能够观察到被解释变量的概率，而该模型的统计估计结果可以用来预测每个个体的概率；
第二步骤：将这些被预测个体概率合并为一个额外的解释变量，与其他控制变量等变量一起来矫正自选择问题。
第二个步骤所提及到合并的额外的解释变量是一个比率，称为逆米尔斯比率（inverse
Mills ration，
例子：在管理学领域，一个典型的问题是企业的某个特征，或者 CEO 的个体特征，对于企业 R&D 投入的影响。在调研抽样过程中也是存在一个样本选择偏差问题：企业的 R&D 投入是企业自愿披露的内容，有的企业不披露，此时做回归时就不能包括这部分缺失的样本（没有披露 R&D 的公司无法观测到他们的 R&D 投入），造成样本选择偏差，结果有偏。这里假设全样本是 1000 家公司，其中 800 家公司披露了其 R&D 投入，即是模型中存在部分 R&D 投入无法观测到的公司样本没有纳入回归，可能会造成由于样本选择偏差而导致的内生性问题从而使得估计结果不一致。接下来采用 Heckman法 来解决这个问题：
第一阶段：采用一个包括全样本（1000家）的 Probit 模型，用来估计一家公司是否会披露其 R&D 投入的概率。这里的因变量是二元的，表示是否披露 R&D 投入；自变量是一些会影响是否披露 R&D 的外生变量，比如其他收入营业收入，杠杆率，公司规模，所属行业等等。然后根据这个 Probit 模型，为每一个样本计算出
， 作用是为每一个样本计算出一个用于修正样本选择偏差的值。（具体怎么计算 后面会推导） 第二阶段：在原来的回归方程，也就是原来只有 800 家公司的样本的方程假如加入
作为控制变量，其他都不变，然后估计出回归参数。这时 的显著性和系数表明了样本选择偏差是否存在以及偏差的方向，如果 是显著，则可以说明样本选择偏差的确影响了你最初模型的估计，这种情况下正好表明了使用 Heckman 两步法纠正样本选择偏差的必要性和接下来需要对样本进行纠正。如果 不显著，说明原模型不存在严重的样本选择偏差，这时 Heckman 第二步得到的结果理论上应该与原模型得到的结果差不多（需要比对一下）。第二步关注的对象是核心解释变量是否显著。只要核心解释变量显著，就说明结果稳健。
因此，我们可以这样简单理解样本选择模型的估计思路：首先，计算全部样本的
3. Heckman两步法步骤理解
上面提及到，其实可以这么理解为：由于样本选择偏差导致的内生性问题本质其实就是遗漏变量的一种特例，这个时候我们要纠正这种偏差，就需要去找到这个缺失的偏差项加入到原回归方程中进行纠正。具体来说就是：
- 第一步：首先采用 probit
方法去估计选择方程，其中原回归方程的被解释变量
是否被观测到或是否取值的虚拟变量 作为 probit 的被解释变量，解释变量包括原回归方程所有解释变量和至少一个外生变量，该外生变量只影响是 否取值，而不影响 的大小，即满足相关性和外生性的要求（但不是工具变量）。估计出所有变量的系数后，将样本数据代入至probit 模型中，计算出拟合值 ，再将 代入风险函数公式（1）中计算出 。 - 第二步 ：将第一步回归计算得到的
作为控制变量引入原回归方程中。如果 显著，说明原回归中存在样本选择偏差，需要使用样本选择模型进行缓解，而其余变量的回归系数则是缓解样本选择偏差后更为稳健的结果；如果 不显著，说明原回归存在的样本选择偏差问题不是很严重，不需要使用样本选择模型，当然，使用了也没关系，因为引入控制变量的回归结果可以与原回归结果比较，作为一种形式的稳健性检验。
4. stata语法介绍
stata 中关于样本选择模型采用的命令是
heckman，这个命令可以实现
heckman两步估计以及模型整体参数的极大似然估计
Basic syntax
1.两步估计法
heckman y x1 x2, select(x1 x2 z1) twostep mills(newname)
or等价于
heckman y x1 x2, select(y_dummy = x1 x2 z1) twostep
----------------------------------------------------------------------------
2.MLE
heckman y x1 x2, select(y_dummy = x1 x2 z1) nolog robust/cluster SE
heckman y x1 x2, select(y_dummy = x1 x2 z1) nolog vce(cluster varname)样本选择模型采用 Heckman 两步法的stata语法大致包括两部分，选择项
select 之前的是第二阶段回归的被解释变量 select
以后指的是对选择方程的具体设置：
select()代表选择方程，括号中的是选择方程的具体变量，有两种写法：（看看上面关于 Heckman 的 Syntax）
- 第一种写法：直接写入控制变量
和外生变量 。此时要求原回归的被解释变量 存在缺失值，这种写法程序会自动识别那些原方程中被解释变量是否是缺失值并且对应生成虚拟变量； - 第二种写法：首先写入被解释变量
是否被观测到的虚拟变量 （ 存在缺失值的样本 标记为 0，不存在缺失值的样本标记为 1，且 取值为 0 不作为缺失值处理）作为选择方程的被解释变量， 等号后面跟着控制变量和外生变量。这种写法需要提前生成 的虚拟变量。 twostep表示使用两步估计法，程序默认使用 MLEmill()表示生成各个样本的，并且以 newname作为变量名nolog表示在使用 MLE 时回归结果不显示迭代过程vce()表示使用稳健标准误，括号中写入robust表示使用的是异方差稳健标准误；若填入cluster varname表示使用聚类稳健标准误，以varname作为聚类标准，一般以经验法则，我们都是要求聚类数目要大于 30 作为聚类的标准，另外vce()不可以在两步法中使用
5. Heckit 案例操作
- 导入数据集
webuse womenwk,clear
*定义全局暂元
global xlist "educ age"
global zlist "married children"
/*
被解释变量: wage
解释变量:educ age
外生解释变量:married children因为样本数据集中的 wage 存在缺失值，所以当我们直接使用
OLS
进行回归的时候可能存在样本选择偏差，因为当使用该数据集的时候因该用样本选择模型
Heckman 两步法进行进一步的稳健性检验。
- 数据处理
tabulate county
County of |
residence | Freq. Percent Cum.
------------+-----------------------------------
0 | 200 10.00 10.00
1 | 200 10.00 20.00
2 | 200 10.00 30.00
3 | 200 10.00 40.00
4 | 200 10.00 50.00
5 | 200 10.00 60.00
6 | 200 10.00 70.00
7 | 200 10.00 80.00
8 | 200 10.00 90.00
9 | 200 10.00 100.00
------------+-----------------------------------
Total | 2,000 100.00该数据集为截面数据，因此标准误无法聚类到个体层面，而同一地区的个体特征可能存在一定的相关性，因此将标准误聚类到county层面，上述结果可以看到，地区数目只有10个，远无法满足聚类数目最低值（30个）的要求，因此选用异方差稳健标准误。
- 查看
的缺失情况和生成虚拟变量
根据 wage 是否存在缺失值生成虚拟变量
wage_dummy 。可以看到，2000个样本中，wage
数据缺失的有657个。并且根据被解释变量是否存在缺失值对应生成虚拟变量
nmissing wage
wage 657
gen wage_dummy=(wage !=.)- 第一个回归：基准回归
reg wage $xlist
est store OLS
Source | SS df MS Number of obs = 1,343
-------------+---------------------------------- F(2, 1340) = 227.49
Model | 13524.0337 2 6762.01687 Prob > F = 0.0000
Residual | 39830.8609 1,340 29.7245231 R-squared = 0.2535
-------------+---------------------------------- Adj R-squared = 0.2524
Total | 53354.8946 1,342 39.7577456 Root MSE = 5.452
------------------------------------------------------------------------------
wage | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
education | .8965829 .0498061 18.00 0.000 .7988765 .9942893
age | .1465739 .0187135 7.83 0.000 .109863 .1832848
_cons | 6.084875 .8896182 6.84 0.000 4.339679 7.830071
------------------------------------------------------------------------------上述第一个回归中，基准回归的结果显示，参与回归的样本数量为1343个，即wage
存在缺失值的样本（657个）在回归时直接被 drop
掉。基准回归中两个解释变量的系数均显著为正，模型拟合程度也较好
- 第二个回归：样本选择模型，使用 MLE 方法进行估计
lambda指的是的估计系数，该值等于 rho和sigma的乘积sigma是原方程干扰项的标准差rho是选择方程干扰项和第二阶段回归干扰项的相关系数。如果rho = 0，表示第二阶段回归中的系数不显著，说明样本选择偏差在原方程中不怎么严重，反之则需要考虑样本选择偏差带来的估计偏误。回归结果的末尾是 LR 检验，检验的原假设是 H0: rho = 0，p 值说明至少可以在 1% 的水平下拒绝原假设，可以认为rho显著不等于0，这说明原模型中确实存在严重的样本选择偏差，基准回归结果不可信。
heckman wage $xlist , select(wage_dummy= $xlist $zlist) nolog mills(imr1)
est store MLE
Heckman selection model Number of obs = 2,000
(regression model with sample selection) Selected = 1,343
Nonselected = 657
Wald chi2(2) = 508.44
Log likelihood = -5178.304 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
wage |
education | .9899537 .0532565 18.59 0.000 .8855729 1.094334
age | .2131294 .0206031 10.34 0.000 .1727481 .2535108
_cons | .4857752 1.077037 0.45 0.652 -1.625179 2.59673
-------------+----------------------------------------------------------------
wage_dummy |
education | .0557318 .0107349 5.19 0.000 .0346917 .0767718
age | .0365098 .0041533 8.79 0.000 .0283694 .0446502
married | .4451721 .0673954 6.61 0.000 .3130794 .5772647
children | .4387068 .0277828 15.79 0.000 .3842534 .4931601
_cons | -2.491015 .1893402 -13.16 0.000 -2.862115 -2.119915
-------------+----------------------------------------------------------------
/athrho | .8742086 .1014225 8.62 0.000 .6754241 1.072993
/lnsigma | 1.792559 .027598 64.95 0.000 1.738468 1.84665
-------------+----------------------------------------------------------------
rho | .7035061 .0512264 .5885365 .7905862
sigma | 6.004797 .1657202 5.68862 6.338548
lambda | 4.224412 .3992265 3.441942 5.006881
------------------------------------------------------------------------------
LR test of indep. eqns. (rho = 0): chi2(1) = 61.20 Prob > chi2 = 0.0000首先，根据上述的回归结果可以看到，选择方程中两个外生变量都是显著为正，说明了外生变量的选择是有效的（第二行
wage_dummy
作为被解释变量的表格）。在第二阶段回归结果中，两个解释变量仍然是显著为正的，且相较于基准回归结果取值变化不是很大，说明在考虑样本选择偏差后的基准回归结果依旧是稳健的。
lambda
的估计系数是 4.2244 ，程序汇报表格最后的是 LR 检验，检验的原假设是
H0: rho = 0，p 值说明至少可以在 1%
的水平下拒绝原假设，可以认为 rho
显著不等于0，这说明原模型中确实存在严重的样本选择偏差，基准回归结果不可信。
第二阶段回归结果中，两个解释变量仍旧显著为正，且相较于基准回归结果取值变化不大，说明考虑到样本选择偏差后基准回归结果依然是稳健的。
回归结果右上角说明总的样本量是 2000 个，参与选择方程回归的样本为 2000 个，参与第二阶段回归的样本为 1343 个。这里是因为第一阶段回归的被解释变量是第二阶段被解释变量是否是缺失值的虚拟变量，所以第一阶段是全样本进行 Probit 回归的，但是第二阶段在把缺失项（逆米尔斯比率项）加入进行回归时，是不需要考虑缺失的样本数据的，因为缺失的样本数据已经在第一部分计算进入了逆米尔斯比率项中，所以第二阶段回归中只有 1343 个样本。
- 第三个回归：样本选择模型，使用 MLE 方法进行估计+异方差稳健标准误
heckman wage $xlist , select(wage_dummy=$xlist $zlist) nolog vce(robust)
est store MLE_r
Heckman selection model Number of obs = 2,000
(regression model with sample selection) Selected = 1,343
Nonselected = 657
Wald chi2(2) = 497.82
Log pseudolikelihood = -5178.304 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| Robust
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
wage |
education | .9899537 .0534141 18.53 0.000 .8852641 1.094643
age | .2131294 .0211095 10.10 0.000 .1717555 .2545034
_cons | .4857752 1.099121 0.44 0.659 -1.668462 2.640013
-------------+----------------------------------------------------------------
wage_dummy |
education | .0557318 .0108899 5.12 0.000 .034388 .0770755
age | .0365098 .0042243 8.64 0.000 .0282303 .0447893
married | .4451721 .0668243 6.66 0.000 .3141988 .5761453
children | .4387068 .0272779 16.08 0.000 .385243 .4921705
_cons | -2.491015 .1884227 -13.22 0.000 -2.860317 -2.121713
-------------+----------------------------------------------------------------
/athrho | .8742086 .1051331 8.32 0.000 .6681514 1.080266
/lnsigma | 1.792559 .0288316 62.17 0.000 1.73605 1.849068
-------------+----------------------------------------------------------------
rho | .7035061 .0531006 .5837626 .7932976
sigma | 6.004797 .1731281 5.674882 6.353893
lambda | 4.224412 .4172197 3.406676 5.042147
------------------------------------------------------------------------------
Wald test of indep. eqns. (rho = 0): chi2(1) = 69.14 Prob > chi2 = 0.0000上述结果显示在使用稳健标准误的回归结果与上文使用普通标准误的回归结果基本保持一致。需要注意的是，在使用稳健标准误后，对
H0: rho = 0的统计检验将变成 Wald 检验，这里 Wald
检验同样拒绝原假设。
- 第四个回归：样本选择模型，使用两步法进行估计
heckman wage $xlist , select(wage_dummy=$xlist $zlist) twostep mills(imr2)
est store twostep
Heckman selection model -- two-step estimates Number of obs = 2,000
(regression model with sample selection) Selected = 1,343
Nonselected = 657
Wald chi2(2) = 442.54
Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
wage |
education | .9825259 .0538821 18.23 0.000 .8769189 1.088133
age | .2118695 .0220511 9.61 0.000 .1686502 .2550888
_cons | .7340391 1.248331 0.59 0.557 -1.712645 3.180723
-------------+----------------------------------------------------------------
wage_dummy |
education | .0583645 .0109742 5.32 0.000 .0368555 .0798735
age | .0347211 .0042293 8.21 0.000 .0264318 .0430105
married | .4308575 .074208 5.81 0.000 .2854125 .5763025
children | .4473249 .0287417 15.56 0.000 .3909922 .5036576
_cons | -2.467365 .1925635 -12.81 0.000 -2.844782 -2.089948
-------------+----------------------------------------------------------------
/mills |
lambda | 4.001615 .6065388 6.60 0.000 2.812821 5.19041
-------------+----------------------------------------------------------------
rho | 0.67284
sigma | 5.9473529
------------------------------------------------------------------------------上述汇报结果显示选择方程引入的外生解释变量是显著的，说明该外生解释变量是有效的，另外原方程回归中的解释变量也是显著的。在第二阶段中，
第二阶段回归结果中，两个解释变量仍旧显著为正，且大小与基准回归结果相比变化不大，这说明在考虑样本选择偏差的情况下，基准回归结果是可信的。
- 第五个回归：手工完成两步估计法
手工计算两步估计法是不推荐的，因为两步估计法下第一步回归的估计误差会带到第二步，造成效率损失，影响第二步估计系数的显著性。
手工两步估计法的思路是先用控制变量和外生变量对
wage_dummy 做 probit 回归，计算出拟合值
*- 第一阶段方程回归（选择方程）
probit wage_dummy $xlist $zlist , nolog
est store first
Probit regression Number of obs = 2,000
LR chi2(4) = 478.32
Prob > chi2 = 0.0000
Log likelihood = -1027.0616 Pseudo R2 = 0.1889
------------------------------------------------------------------------------
wage_dummy | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
education | .0583645 .0109742 5.32 0.000 .0368555 .0798735
age | .0347211 .0042293 8.21 0.000 .0264318 .0430105
married | .4308575 .074208 5.81 0.000 .2854125 .5763025
children | .4473249 .0287417 15.56 0.000 .3909922 .5036576
_cons | -2.467365 .1925635 -12.81 0.000 -2.844782 -2.089948
------------------------------------------------------------------------------上面说了在第一阶段选择方程回归的样本数量是 2000 个的原因，上述手工回归的第一阶段 probit 回归中，控制变量和外生解释变量都是显著为生，说明外生解释变量的选定是有效的。
接着根据拟合值 normalden() 是标准正态的概率密度函数
pdf ，normal() 是标准正态的累积分布函数
cdf：
*计算imr值
predict y_hat, xb
gen imr=normalden(y_hat)/normal(y_hat)在上面计算各个样本的
*- 第二阶段方程回归
reg wage $xlist imr
est store second
Source | SS df MS Number of obs = 1,343
-------------+---------------------------------- F(3, 1339) = 173.15
Model | 14913.1368 3 4971.04559 Prob > F = 0.0000
Residual | 38441.7579 1,339 28.7093039 R-squared = 0.2795
-------------+---------------------------------- Adj R-squared = 0.2779
Total | 53354.8946 1,342 39.7577456 Root MSE = 5.3581
------------------------------------------------------------------------------
wage | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
education | .9812232 .0504379 19.45 0.000 .8822772 1.080169
age | .2167985 .0209799 10.33 0.000 .1756415 .2579555
imr1 | 4.079591 .5864901 6.96 0.000 2.929051 5.23013
_cons | .5372467 1.183409 0.45 0.650 -1.784291 2.858785
------------------------------------------------------------------------------- 比对各个方法计算的
*- 对比imr、imr1和imr2
order imr1 imr2 imr wage_dummy //排序所有样本的IMR均有取值。
- 对比五个模型的回归结果
local mlist "OLS MLE MLE_r twostep first second"
esttab `mlist' using 样本选择模型.rtf, replace ///
b(%6.4f) t(%6.4f) ///
scalar(N r2_a r2_p) compress nogap ///
star(* 0.1 ** 0.05 *** 0.01) ///
mtitle(`mlist') ///
title("Sample Selection Model")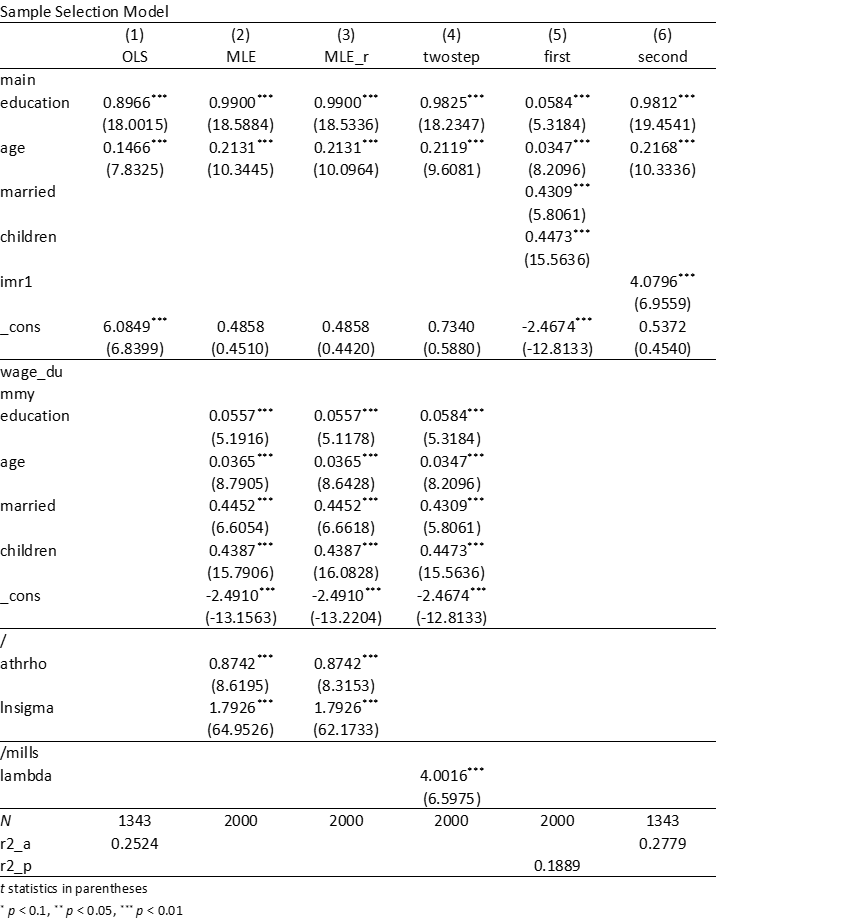
通过上述五个模型回归的结果分析，可以发现以下结论：
- 两个解释变量（
education和age）的回归系数的符号、大小、显著性在模型(2)(3)(4)(6)中基本保持一致，并且与模型(1)(基准回归)的区别不大，这说明在考虑到样本选择偏差后，根据基本回归结果得出的结论依然成立。- 模型(2)(3)(4)汇报的样本量是2,000个全样本，但应该清楚不同回归阶段实际参与的样本数目是不同的。
以上命令、代码和实例均基于截面数据，现阶段的文献大多数也是将面板数据转为截面数据处理，最多控制几个个体虚拟变量和时间虚拟变量，并将其视为面板数据回归。
- 估计面板数据的stata命令
Stata在16及以上版本中提供了估计面板数据样本选择模型官方命令xtheckman，但这个命令只能估计随机效应模型，估计固定效应模型需安装一个外部命令
xtheckmanfe，可以键入如下代码进行安装或更新。
ssc install xtheckmanfe, replace6. 论文案例
依旧会采用中国工业经济的论文案例来说明，Heckman两步法在一篇论文中的位置
郭玥.政府创新补助的信号传递机制与企业创新[J].中国工业经济,2018(09):98-116.DOI:10.19581/j.cnki.ciejournal.2018.09.016.
在稳健性检验中，未来避免由于信息缺漏而造成估计的偏误，对于年报中明确报告研发经费项目无或者为零的企业，研发投入变量赋值为0，而未披露研发经费支出项目的企业，研发投入变量按缺漏值处理，这样选取研发投入作为被解释变量意味着自动忽略了那些没有研发行为的样本，这种非随机的样本选择会导致最终的估计有偏。于是这篇论文是考虑到具有研发行为的企业会有申请创新补助的动机，是否有研发行为和是否申请创新补助在决策上具有一致性。
为解决样本选择偏误问题，论文采用 Heckman 两步法，具体的回归模型如下：
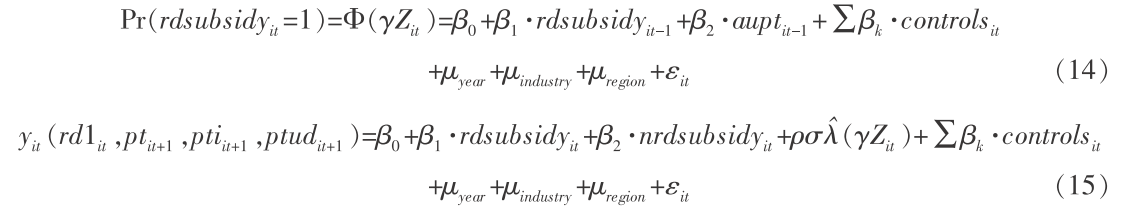
方程（14）是一个probit模型用于估计
global x "rdsubsidy nrdsubsidy" //全局暂元定义核心解释变量
global control "size age lev fasset growth holderr1 bsmsalary market" //全局暂元定义控制变量
global select "select(rdsubsidy_dum = lsubsidy llnptinf $control _Iy* _a* _h*) twostep" //全局暂元定义选择方程和确定两步估计法，_Iy* _a* _h*固定效应
*原基准回归，没有考虑样本选择偏差的内生性问题
qui xtreg rd1 $x $control _Iy*, fe r
est store rd1_OLS
*利用heckman两步法回归，考虑了样本选择偏差问题
qui heckman rd1 $x $control _Iy* _a* _h*, $select
est store rd1_Heckman
local mm "rd1_OLS rd1_Heckman"
esttab `mm', mtitle(`mm') compress nogap star(* 0.1 ** 0.05 *** 0.01) b(%12.4f) t(%12.4f) drop(_I* _a* _h* $control _cons)
/*结果汇报：
------------------------------------
(1) (2)
rd1_OLS rd1_Hec~n
------------------------------------
main
rdsubsidy 0.1932*** 0.7195***
(4.9457) (21.6573)
nrdsubsidy 0.0652** 0.1896***
(2.3337) (6.0854)
------------------------------------
rdsubsid~m
lsubsidy 0.0894***
(4.7023)
llnptinf 0.1779***
(21.7316)
------------------------------------
/mills
lambda -1.7654***
(-14.0452)
------------------------------------
N 11835 12125
------------------------------------*/从汇报的结果显示，lambda
值是显著为负，说明原来的基准回归是存在把不可忽视的样本选择偏差问题，利用heckman两步法进行回归后发现，处理后的列（2）的回归系数
0.7195 要远大于原基准回归的列（1） 的 0.1932。