倾向得分匹配PSM
倾向得分匹配PSM
1. 选择偏差与内生性
自选择问题:模型中的核心解释变量不是随机分配的,而是个体可以自主选择的,比如在研究培训对求职的帮助时,求职者可以自主选择是否参加培训;各地区对是否实施政策有着自己的“小九九”。
- 例子:评估一项污染防治政策的政策效果,选择期初污染程度基本一致的地区作为样本,并根据各地区意愿决定其是否实施该项政策,3年后政策实施地的污染指标明显低于未实施该政策的地区,结论是这项政策有效。
自选择性偏误:上述例子存在的问题是影响某地是否实施政策的变量
D 的选择(
2. 随机分组和自选择性偏差
假设要评估一项政策的实施试验效果:上大学对收入增加的效应有多大?即是要考察个体
于是为了使得
但是如果我们可以找到决定个体是否参与实验的因素,然后在控制组中匹配到这些因素与处理组相等的样本,最后将这些样本作为我们真正参与评估的控制组,这样子就可以做到个体被处理的选择近似随机。所以当影响个体选择是否参与处理的罂粟是可观测时,个体的决策就是依可观测变量选择;当决定个体是否参与实验的因素是不可观测因素时,个体的决策就是依不可观测变量选择。由于不可观测因素不可度量,而将控制组样本与处理组样本匹配时需要准确识别出这些因素,因此我们对于能够将控制组和处理组的样本匹配仅仅只讨论基于可观测变量(协变量)来设计的,而倾向得分匹配的则是个体与个体之间的协变量。
graph TB
估计ATT最理想的方法是找到参与实验的个体在平行时空的自己,并假设平行时空的自己没有参与实验,最后作差得出最纯粹的ATT--但是找到平行时空的自己不现实-->可以使用随机分组的处理组与控制组,作差得到ATT--但现实中个体是否参与实验的选择不随机-->找出影响个体是否参与实验的因素,控制两组间因素的取值相等,最后利用处理后的分组样本作差得到ATT3. 倾向得分匹配
决定个体是否被处理的因素是协变量,而当协变量是单一变量时,我们只需要在控制组找到与处理组协变量取值相等的样本作为我们的被匹配对象;但是需要被匹配的对象的协变量并非单一,而是一个由多个协变量构成的多维向量
PSM的主要步骤:
- 选择协变量。多数论文直接将基础回归所使用的控制变量作为协变量,这种做法的基本逻辑在于要求协变量与
相关,但问题在于这些控制变量不一定与处理组变量 相关,即便相关,也可能是协变量的高次项或交互项与 相关。 - 估计倾向得分值。作为被解释变量,协变量作为解释变量,由于D是一个二元哑变量,因此使用
logit模型或probit模型,应用中更多使用logit模型。logit回归之后会得到各个样本的倾向得分值(在psmatch2中将生成_pscore变量,_pscore介于 [0,1] 之间),之后就是根据_pscore进行第三步的匹配。- 根据
_pscore进行匹配。匹配的方法有:卡尺最近邻匹配、半径匹配、核匹配。最常用的是卡尺最近邻匹配,卡尺最近邻匹配基于最近邻匹配,最近邻匹配需要设置邻居数(neighbor(#1)),也就是说根据倾向得分值最接近的原则,每一个处理组样本匹配到#1个控制组样本,但如果控制组样本的倾向得分值与处理组样本差距太大,这样的匹配是没有多大意义的,因此需要还设置一个卡尺(caliper(#2)),即控制一个阈值界限,界限内的控制组样本可以作为匹配对象,界限外的样本则被忽视。
尽管PSM通过匹配再抽样的方法使得观测数据尽可能地接近随机实验数据,在很大程度上能够减少观测数据的偏差,但是PSM存在以下假设,这些假设也是psm在应用中的局限性:
- 服从条件独立假设
条件独立假设(conditional independence)是一个较为严格的假定,意味着回归方程不存在遗漏变量的问题。如果存在不可观测的遗漏变量,那么PSM的结果可能是存在问题的。
- 服从共同支撑假设
共同支撑假设(common support)要求处理组和对照组的倾向得分有较大的共同取值范围。如果共同取值范围过小,那么数据可能不适合做倾向得分匹配。
3. PSM+DID
其实倾向得分匹配和双重差分是一对好基友
因为我们在对政策进行效应评估的时候,为了保证估计结果的一致性,需要保证处理组的随机处理否则会出现自选择偏差的问题,但是现实往往确实无法保证政策实施的随机试验。而当我们使用 PSM 方法的时候却可以很巧妙地为每一个处理组的匹配到特定的控制组样本(通过倾向得分构造处理组的反事实对照组),使得匹配下的准自然试验近似随机。
但是PSM本质上只适用于截面数据,每一个处理组样本匹配到的时同一个时间节点的控制组样本,得到的
- 将面板数据视为截面数据再匹配
- 逐期匹配
4. PSM匹配方式
倾向得分匹配的具体方法主要包括以下三种:
- 近邻匹配
近邻匹配(nearest neighbor matching)通过在对照组中寻找倾向得分最接近处理组的个体进行匹配。也就是这篇笔记后面所使用到的最近邻匹配方法,近邻匹配也分为一对一匹配和一对多匹配
*One-to-one matching:
psmatch2 D x1 x2 x3 , outcome(y) caliper(real) noreplacement common odds index logit ties ate
/*
noreplacement指的是不放回匹配,只限定在1:1匹配中
ties指的是包括所有倾向性得分相同的并列个体,默认按数据顺序选择其中的一位个体
common表示仅对共同取值范围(common support)内个体进行匹配,默认对所有个体进行匹配
odds表示使用几率比(odds ratio,即是p/(1-p)进行匹配),默认使用倾向性得分p进行匹配
*/
*k-Nearest neighbors matching:
psmatch2 D x1 x2 x3 , outcome(y) neighbor(integer k>1) caliper(real) common odds logit ties ate- 卡尺匹配/半径匹配
卡尺匹配(caliper matching)也称为半径匹配(radius matching),设定倾向得分差距的绝对值作为卡尺范围/半径范围,将得分值差异在卡尺范围内的不同组个体进行配对。简单理解就是先根据处理组的得分为中心设置一个半径(caliper的值),然后按照这个半径里面出现的控制组的样本进行均值匹配
*Radius matching:
psmatch2 D x1 x2 x3 , outcome(y) radius caliper(real) common odds logit ate
//radius表示的是半径匹配- 核匹配
核匹配(kernel matching)对每一个处理组的个体都使用对照组个体作为匹配。根据对照组个体与处理组个体i距离的不同赋予不同的权重,与个体i距离越近的权重越高,距离越远的权重越低,权重由核函数计算得出。离我更近的个体给予权重更大,因为更近的个体意味着具有越多的信息。
*Kernel matching:
psmatch2 D x1 x2 x3 , outcome(y) kernel kerneltype(kernel_type) bwidth(real) common odds logit ate匹配方法的选择由具体数据决定,不同的数据类型对应的是不同的匹配方法,我们需要尝试不同的方法并对结果进行比较。除了上述讲到最常用的方法匹配方法以外,还有
Local linear regression matching、spline
matching等等,具体实现命令可以通过 help psmatch2 查阅。
5. PSM案例实现
李青原, 章尹赛楠. 金融开放与资源配置效率——来自外资银行进入中国的证据[J]. 中国工业经济, 2021(05): 95-113.
1. 数据处理
cd E:\Users\置上\Desktop\数据
*===设置图片输出样式===
graph set window fontface "Times New Roman"
graph set window fontfacesans "宋体"
set scheme s1color
use 行业数据.dta, clear
*===定义全局暂元===
global xlist "ADM PPE ADV RD HHI INDSIZE NFIRMS FCFIRM MARGIN LEVDISP SIZEDISP ENTRYR EXITR"
global regopt "absorb(city ind3) cluster(city#ind3 city#year) keepsing"
*===生成处理组虚拟变量===
gen treated = ( city == 5101 | city == 5000 | city == 2102 | city == 3501 ///
| city == 4401 | city == 3701 | city == 3201 | city == 3702 ///
| city == 3101 | city == 4403 | city == 1200 | city == 4201 ///
| city == 4404 | prov == 44 | prov == 45 | prov == 43 ///
| prov == 32 | prov == 33 | city == 1100 | city == 5301 ///
| city == 2101 | city == 3502 | city == 6101 | city == 2201 ///
| city == 2301 | city == 6201 | city == 6401 )
save psmdata.dta, replace2. 截面PSM和DID
- 安装
psmatch2的外部命令
ssc install psmatch2,replace- 设置随机种子和匹配
在正式使用 psmatch2
前,需要设置一个随机种子并将样本进行随机排序,原因是当在匹配控制组样本时,如果有几个样本的倾向得分值是一样的,那么程序会优先根据随机生成的排序靠前的样本
*注意:这里是截面匹配
use psmdata.dta, clear
*===卡尺最近邻匹配(1:2)===
set seed 0000
gen norvar_1 = rnormal()
sort norvar_1
psmatch2 treated $xlist , outcome(TFPQD_OP) logit neighbor(2) ties common ate caliper(0.05)
save csdata.dta, replace
treated是本例中的分组变量。$xlist是协变量的全局暂元(这里直接使用基础回归中的控制变量),实际使用中要结合其他文献及敏感性分析挑选出适合的协变量outcome(TFPQD_OP)的括号中指的是结果变量(TFPQD_OP),即是基准回归中的被解释变量logit表明的是采用 logit 模型进行倾向得分值得估计,一般程序默认使用 probitneighbor(2)表明使用得是最近邻匹配,括号填入 2 说明采用得匹配方法,即是一个处理组样本最多可以匹配两个控制组样本 ties说明当存在多个控制组样本得倾向得分值相同并且这个得分值对应的样本应该被匹配时,那么匹配得样本得结果变量取他们的均值common表示只对倾向得分值共同取值范围内的样本进行匹配。也就是说,以开始我限定了一个大的倾向得分值的取值范围,如果两组样本的倾向得分值如果不在共同取值范围内,则直接被排除,从一开始就没有匹配资格。默认对所有样本进行匹配。ate表示同时汇报、 和 ,默认只汇报 caliper(0.05)表示最近邻的卡尺设置为0.05,即控制组样本的倾向得分值如果在处理组样本倾向得分值 ±0.05 以内,才能有被匹配的资格。因此,如果选择项同时包括neighbor(#)和caliper(#),则说明使用卡尺最近邻匹配。
结果分析:
Logistic regression Number of obs = 81,567
LR chi2(13) = 5973.89
Prob > chi2 = 0.0000
Log likelihood = -53407.844 Pseudo R2 = 0.0530
------------------------------------------------------------------------------
treated | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
ADM | 2.303432 .1007328 22.87 0.000 2.105999 2.500865
PPE | -1.222116 .0342674 -35.66 0.000 -1.289279 -1.154953
ADV | 21.56327 3.731756 5.78 0.000 14.24917 28.87738
RD | 18.12885 3.306851 5.48 0.000 11.64754 24.61016
HHI | -.4729895 .065837 -7.18 0.000 -.6020276 -.3439513
INDSIZE | .0015667 .0103893 0.15 0.880 -.018796 .0219294
NFIRMS | .4045981 .0190289 21.26 0.000 .3673021 .441894
FCFIRM | 2.685802 .1414342 18.99 0.000 2.408596 2.963008
MARGIN | .8316006 .0620282 13.41 0.000 .7100276 .9531736
LEVDISP | -2.178396 .0987579 -22.06 0.000 -2.371958 -1.984835
SIZEDISP | .2341893 .0247433 9.46 0.000 .1856934 .2826852
ENTRYR | -.0103419 .0385426 -0.27 0.788 -.0858841 .0652002
EXITR | -.1123095 .0605613 -1.85 0.064 -.2310075 .0063884
_cons | -.9478736 .1123736 -8.44 0.000 -1.168122 -.7276253
------------------------------------------------------------------------------
----------------------------------------------------------------------------------------
Variable Sample | Treated Controls Difference S.E. T-stat
----------------------------+-----------------------------------------------------------
TFPQD_OP Unmatched | 2.24921913 2.35179198 -.102572852 .006214925 -16.50
ATT | 2.24921615 2.35605481 -.106838668 .008017304 -13.33
ATU | 2.35179488 2.28215595 -.069638929 . .
ATE | -.089340447 . .
----------------------------+-----------------------------------------------------------
Note: S.E. does not take into account that the propensity score is estimated.
psmatch2: | psmatch2: Common
Treatment | support
assignment | Off suppo On suppor | Total
-----------+----------------------+----------
Untreated | 1 38,367 | 38,368
Treated | 1 43,198 | 43,199
-----------+----------------------+----------
Total | 2 81,565 | 81,567psmatch2 命令回归后程序汇报了三个表格:
- 表格 1 汇报的是 logit 模型回归的结果,意义不大;
- 表格 2 需要重点关注
ATT的大小和显著性。在没有匹配之前的Unmatched,平均处理效应是 -0.1026,并且是在 1% 下显著的(t值的绝对值大于2.58);但是在匹配之后的参与者平均处理效应ATT是 -0.1068,同样是在 1% 下显著。注意:这个的ATT结果仅仅是参与者实施政策对结果变量的影响,而双重差分只在界面维度进行差分,并没有考虑时间维度的差分; - 表格 3
汇报了两组在共同取值范围内的样本量(
On support那一列)。处理组和控制组都分别只有一个样本在共同取值范围外,说明绝大多数样本(特别是控制组样本)都有资格参与匹配。打开数据编辑器,可以找到是处理组存在一个极端小的得分值(0.128248)和控制组存在一个极端大的得分值(0.944485)这两个极端值其实已经超过了一开始我们设定的共同取值范围(倾向得分值最大最小值的取值范围)。
- 平衡性检验
平衡性检验(Balance
Test):检验匹配后协变量取值在两组间(Unmatched 和
matched
)是否存在显著差异,如果协变量取值差异不明显,即是个体用于匹配的特征变量几乎没什么差异,则说明匹配效果好,所以使用这样的匹配样本近似准自然试验进行DID回归就比较合适。
平衡性检验分为两种情况:
- 一是度量两组间协变量的标准化均值的偏差
%bias。如果匹配后协变量的%bias小于10%,且明显小于未匹配前的%bias,则说明对于这个协变量来说,两组间并无差距。- 二是通过 t 检验来判断各个协变量的取值在两组间是否存在系统性偏差。t 检验的原假设(
H0)是:两组间协变量的取值不存在系统性偏差,因此我们的目标是最终接受H0,即是想要统计量不显著才可以说明匹配后的两组间协变量没什么差异。
/*psmatch2自带两个估计后检验命令:
1. pstest:用于进行平衡性检验;
2. psgraph:用柱状图的方式直观呈现出两组间满足共同支撑假设(即倾向得分值在共同取值范围内)样本分布情况*/
*平衡性检验
pstest, both graph saving(balancing_assumption, replace)
*共同支撑假设检验
psgraph, saving(common_support, replace)pstest 汇报结果分析:
----------------------------------------------------------------------------------------
Unmatched | Mean %reduct | t-test | V(T)/
Variable Matched | Treated Control %bias |bias| | t p>|t| | V(C)
--------------------------+----------------------------------+---------------+----------
ADM U | .07524 .06583 11.5 | 16.40 0.000 | 1.07*
M | .07524 .07762 -2.9 74.7 | -3.92 0.000 | 0.77*
| | |
PPE U | .34533 .40875 -29.7 | -42.32 0.000 | 0.93*
M | .34532 .34725 -0.9 96.9 | -1.36 0.173 | 1.02*
| | |
ADV U | .00044 .00036 4.4 | 6.22 0.000 | 1.26*
M | .00044 .00042 1.1 75.5 | 1.50 0.133 | 1.03*
| | |
RD U | .00047 .0003 6.9 | 9.77 0.000 | 1.63*
M | .00047 .00045 0.5 92.1 | 0.72 0.470 | 1.03*
| | |
HHI U | .2341 .26739 -19.8 | -28.19 0.000 | 0.95*
M | .23409 .23365 0.3 98.7 | 0.38 0.703 | 0.97*
| | |
INDSIZE U | 13.279 12.873 29.9 | 42.60 0.000 | 1.01
M | 13.279 13.291 -0.9 96.9 | -1.31 0.189 | 0.85*
| | |
NFIRMS U | 2.6806 2.3742 37.9 | 53.74 0.000 | 1.35*
M | 2.6807 2.6892 -1.1 97.2 | -1.41 0.159 | 0.89*
| | |
FCFIRM U | .01606 .00744 15.2 | 21.47 0.000 | 2.16*
M | .01606 .01534 1.3 91.7 | 1.60 0.109 | 1.01
| | |
MARGIN U | .8387 .83491 2.9 | 4.17 0.000 | 1.01
M | .8387 .83786 0.6 77.9 | 0.95 0.343 | 0.99
| | |
LEVDISP U | .25657 .26916 -16.9 | -24.11 0.000 | 0.81*
M | .25656 .25834 -2.4 85.9 | -3.69 0.000 | 0.99
| | |
SIZEDISP U | 1.211 1.1797 8.3 | 11.88 0.000 | 0.85*
M | 1.211 1.2131 -0.5 93.4 | -0.83 0.405 | 0.97*
| | |
ENTRYR U | .081 .08743 -3.4 | -4.82 0.000 | 0.92*
M | .081 .07818 1.5 56.1 | 2.25 0.024 | 1.05*
| | |
EXITR U | .03935 .0459 -5.4 | -7.74 0.000 | 0.81*
M | .03935 .04031 -0.8 85.4 | -1.21 0.225 | 0.96*
| | |
----------------------------------------------------------------------------------------
* if variance ratio outside [0.98; 1.02] for U and [0.98; 1.02] for M
-----------------------------------------------------------------------------------
Sample | Ps R2 LR chi2 p>chi2 MeanBias MedBias B R %Var
-----------+-----------------------------------------------------------------------
Unmatched | 0.053 5936.79 0.000 14.8 11.5 55.2* 1.17 85
Matched | 0.000 45.01 0.000 1.1 0.9 4.6 0.91 77
-----------------------------------------------------------------------------------
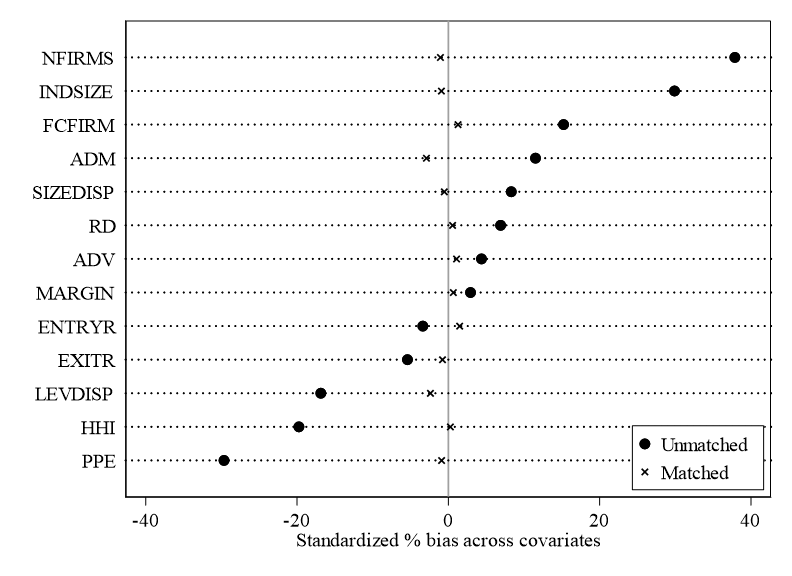
* if B>25%, R outside [0.5; 2]pstest 汇报了两个表、一张 %bias 图:
第一个表汇报了各个协变量的
Unmatched和matched下的%bias,可以发现在匹配之后的matched的%bias都是小于 10% ,且是小于匹配之前的%bias,%bias的绝对值较匹配前大幅下降了56.1%~98.7%;除ADM、LEVDISP和ENTRYR这三个协变量拒绝原假设外,其余协变量均不拒绝“两组间协变量的取值不存在系统性偏差”的原假设,即是只有ADM、LEVDISP和ENTRYR这三个协变量在匹配的两组间存在系统性偏差。第二张表汇报了匹配前后的 logit 回归的情况,其中
Unmatched那一行是匹配前的回归结果,Matched那一行是匹配后的logit回归情况。结果显示:匹配后回归结果中伪R方(Ps R2)明显变小,这说明匹配后两组间的所有协变量取值差异性都不大,从而对 logit 回归中的被解释变量的变动没有太大的解释力。
%bias图:呈现了各个协变量的Unmatched和matched下的%bias差异,可以发现在匹配后的两相对于没有匹配之前的偏差会更小(%bias都小于 10% ),其中ADM、LEVDISP和ENTRYR是这些协变量中偏差最大但是依旧符合%bias都是小于 10% 的要求。
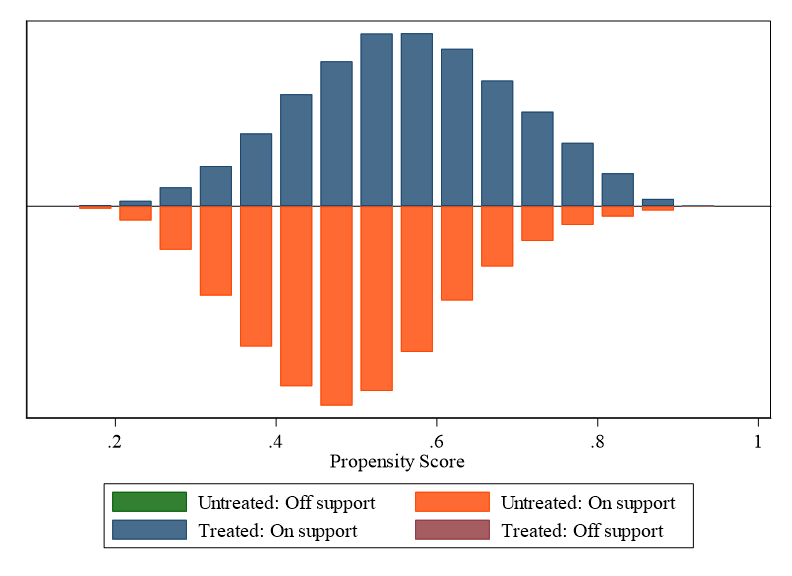
psgraph 汇报结果:
和前文 psmatch2
运行结果中的第三张表保持一致,即处理组和控制组的绝大多数样本都在共同取值范围内可以互相进行匹配,而对于那些无法匹配的倾向得分值排除在了共同取值范围以外,说明这类样本的倾向得分值比较极端(从图片中暂时无法看出是极端大还是极端小)。
Unmatched 和 matched
倾向得分值的核密度图比较:
如果匹配前两组间的核密度曲线偏差比较大,而匹配后核密度曲线比较接近,说明匹配效果好。
*倾向得分值的核密度图
sum _pscore if treated == 1, detail //处理组的倾向得分均值为 0.5632
*- 匹配前
sum _pscore if treated == 0, detail //未被处理组的倾向得分均值为 0.4918241
*这里只画出treated == 1和treated == 0的倾向得分值核密度图,代表的是匹配之前的二者得分分布是否近似
twoway(kdensity _pscore if treated == 1, lpattern(solid) ///
lcolor(black) ///
lwidth(thin) ///
scheme(qleanmono) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", ///
size(medlarge) orientation(h)) ///
xtitle("{stSans:匹配前的倾向得分值}", ///
size(medlarge)) ///
xline(0.5632 , lpattern(solid) lcolor(black)) ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
saving(kensity_cs_before, replace)) ///
(kdensity _pscore if treated == 0, lpattern(dash)), ///
xlabel( , labsize(medlarge) format(%02.1f)) ///
ylabel(0(1)4, labsize(medlarge)) ///
legend(label(1 "{stSans:处理组}") ///
label(2 "{stSans:控制组}") ///
size(medlarge) position(1) symxsize(10))
*- 匹配后
sum _pscore if treated == 0 & _weight != ., detail //没有被处理并且是被匹配过的样本倾向得分值是0.5109521
*这里只画出treated == 1和treated == 0 & _weight != .的倾向得分值核密度图,代表的是匹配之后处理组和处理组匹配的控制组样本的倾向得分值是否近似
twoway(kdensity _pscore if treated == 1, lpattern(solid) ///
lcolor(black) ///
lwidth(thin) ///
scheme(qleanmono) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", ///
size(medlarge) orientation(h)) ///
xtitle("{stSans:匹配后的倾向得分值}", ///
size(medlarge)) ///
xline(0.5632 , lpattern(solid) lcolor(black)) ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
saving(kensity_cs_after, replace)) ///
(kdensity _pscore if treated == 0 & _weight != ., lpattern(dash)), ///
xlabel( , labsize(medlarge) format(%02.1f)) ///
ylabel(0(1)4, labsize(medlarge)) ///
legend(label(1 "{stSans:处理组}") ///
label(2 "{stSans:控制组}") ///
size(medlarge) position(1) symxsize(10))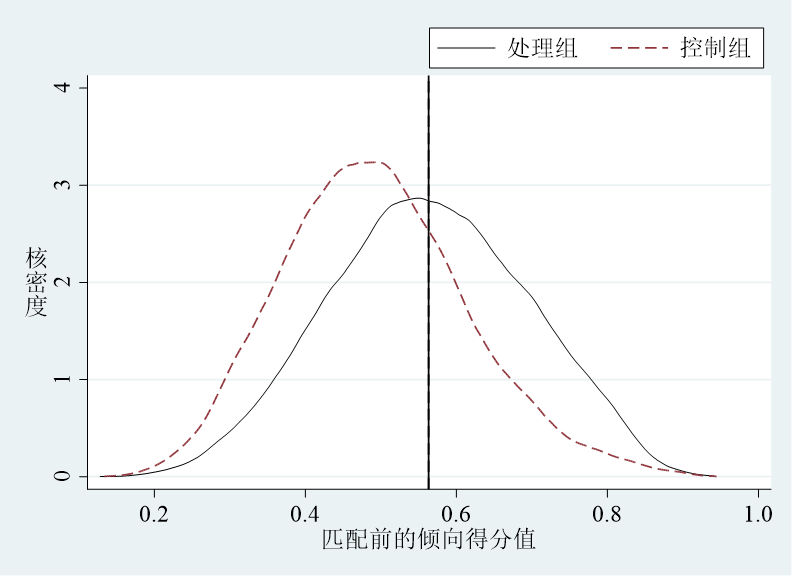
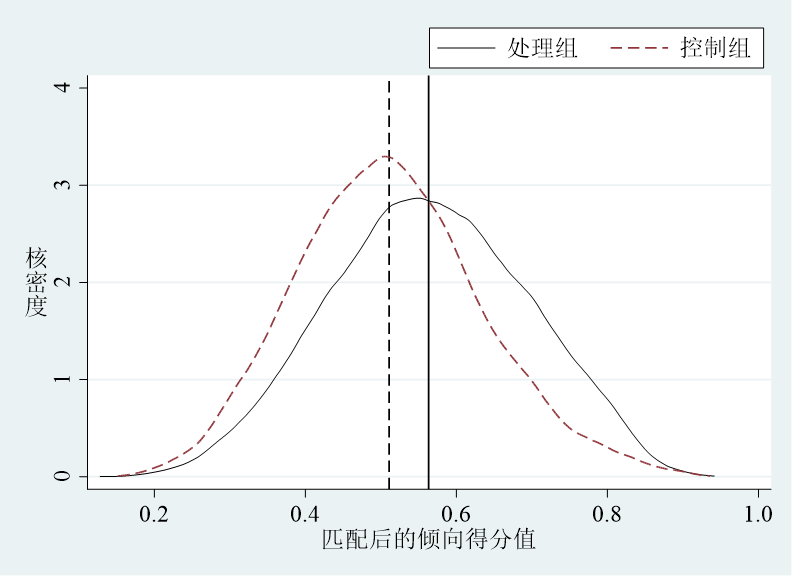
从匹配前的处理组和未被处理的倾向得分值核密度曲线与匹配后处理组和处理组匹配的控制组样本的核密度曲线做对比,可以发现匹配前后两条核密度曲线偏差都较大,但是匹配后两条曲线更为接近了。从一定程度上可以说明我们的匹配还是有效果。
psmatch2生成变量解释和回归
对于 psmatch2 在数据集中生成了几个新变量的变量解释:

_pscore是样本经过 logit 模型计算的倾向得分值;
_treated是样本是否是处理组的虚拟变量,_treated=1是被处理组
_support是样本是否满足共同支撑假设的虚拟变量,_support=1即如果样本处于共同取值范围内,否则为0。
_weight是关于对照组和控制组匹配的关键变量,体现了是否匹配成功和匹配的次数
对于处理组样本而言:
_weight为空时存在两种情况:(1)没有参与匹配(即未满足共同支撑假设);(2)参与匹配但在卡尺范围内暂未匹配到控制组样本。如果匹配成功了,该变量取值为1。对于控制组样本而言:
_weight为空说明:样本不满足共同支撑假设或在卡尺范围内没有匹配成功;对于匹配成功的样本,该变量可能取整也可能不取整,这取决于样本匹配成功的次数。具体来说分成放回匹配和不放回匹配:
如果是
1:1无放回匹配,则每个处理组样本最多匹配成功一次,并且控制组样本也最多被匹配一次,因此对于控制组中匹配成功的样本来说,_weight只能等于1;如果是
1:1有放回匹配,则每个处理组样本最多匹配成功一次,而控制组样本可能被匹配 k 次,因此对于控制组中匹配成功的样本来说,_weight的取值为大于等于 1 的整数;如果是1:m的有放回匹配(psmatch2只允许在1:1匹配中设置无放回选项),则一个处理组样本最多可以匹配到 m 个对象,因此被匹配到的对象所占的权重为,那么对于控制组样本来说,如果它被匹配到了 k 次,那么它的总权重就是 ,即 _weight取值为。如果我们想要知道在 1:m有放回匹配中,控制组样本被匹配的次数 k,那么就只要将它们的_weight乘以 m 即可。因此,
_weight的取值表明了样本是否参与匹配以及样本的重要性程度。
_TFPQD_OP代表样本匹配到对象的结果变量(TFPQD_OP)的均值(因为预设了当匹配多个未被处理的控制组时采取取均值作为最后的匹配对象的结果变量)
_id是psmatch2自动为每一个样本赋予的唯一识别编码
_n1和_n2代表样本匹配对象在_id中的编码,由于这里是1:2匹配,所以分别代表连个匹配对象的_id编码
_nn表示处理组样本匹配到的控制组样本的个数
_pdif表示样本的倾向得分值与_n1样本倾向得分值之差的绝对值
总的来说,基本上主要样本中的 _weight
不是空值,代表了该样本参与了匹配,就可以将这些样本放入到双重差分中进行参数估计,并且可以在一定程度上缓解了基准回归中存在选择偏差问题,还可以作为稳健性检验来验证基准回归的结果。
可是,我们需要重视在通过 PSM 构造的被匹配的控制组样本可能作为多个处理组样本的匹配对象,因为不同权重的控制组样本在总体上的控制组样本中的重要性程度是不一样的。权重越大,说明被匹配上的次数越多,参与回归时越应该被重视,因此一种可行的办法是根据权重来复制控制组中被匹配上的样本(频数加权回归)。
所以,在进行回归结果对比时,除了需要包括两个基准回归、一个使用权重不为空的样本进行的回归和一个使用使用满足共同支撑假设的样本进行的回归,还需要包括一个考虑样本重要性的频数加权回归。
**回归结果对比
*基准回归1(混合OLS)
qui: reg TFPQD_OP FB $xlist , cluster(city)
est store m1
*基准回归2(固定效应模型)
qui: reghdfe TFPQD_OP FB $xlist , $regopt
est store m2
*PSM-DID1(使用权重不为空的样本)
qui: reghdfe TFPQD_OP FB $xlist if _weight != ., $regopt
est store m3
*PSM-DID2(使用满足共同支撑假设的样本)
qui: reghdfe TFPQD_OP FB $xlist if _support == 1, $regopt
est store m4
*PSM-DID3(使用频数加权回归)
gen weight = _weight * 2
replace weight = 1 if treated == 1 & _weight != .
qui: reghdfe TFPQD_OP FB $xlist [fweight = weight], $regopt
est store m5
*频数加权回归的另外一种思路:
gen weight = _weight * 2
replace weight = 1 if treated == 1 & _weight != .
keep if weight != .
expand weight
reghdfe TFPQD_OP FB $xlist , $regopt
est store m5
*回归结果输出
local mlist_1 "m1 m2 m3 m4 m5"
reg2docx `mlist_1' using 截面匹配回归结果对比.docx, b(%6.4f) t(%6.4f) ///
scalars(N r2_a(%6.4f)) noconstant replace ///
mtitles("OLS" "FE" "Weight!=." "On_Support" "Weight_Reg") ///
title("基准回归及截面PSM-DID结果")可以看到,核心解释变量外资银行进入(FB)在五个回归中均显著为负,且第(3)(4)(5)列FB系数值大小与第(2)列相差不大,其余控制变量的系数也符合预期,这说明当考虑到选择偏差问题后,基准回归结果依旧稳健。
此外,观察各回归中实际参与回归的样本数N可以发现,因为第(3)列使用的是权重不为空的样本,即PSM匹配成功的样本,因此样本量相比基础回归有所减少,且减少幅度较大;第(3)列使用的是满足共同支撑假设的样本,由于只有两个样本不满足假设,因此参与回归的样本只比基础回归少两个;第(4)列由于是根据权重进行的频数加权回归,实际参与回归的样本会根据权重进行复制,因此最终有116,882个样本参与回归。
--------------------------------------------------------------------------------------------
(1) (2) (3) (4) (5)
OLS FE Weight!=. On_Support Weight_Reg
--------------------------------------------------------------------------------------------
FB -0.1243*** -0.0496*** -0.0545*** -0.0497*** -0.0422***
(-5.2480) (-3.6531) (-3.9823) (-3.6550) (-2.9228)
ADM 1.0682*** 0.8719*** 0.9287*** 0.8719*** 0.9839***
(17.6388) (18.0260) (16.1842) (18.0262) (12.0535)
PPE -0.1183*** -0.0845*** -0.0784*** -0.0845*** -0.0813***
(-4.3488) (-5.4869) (-4.3384) (-5.4864) (-3.6168)
ADV 3.4239* 0.4029 1.6045 0.3975 2.3618
(1.9284) (0.2547) (0.8734) (0.2513) (0.9525)
RD -1.1993 -3.5116*** -3.4516** -3.4852*** -4.2360*
(-0.8120) (-2.6572) (-2.1919) (-2.6371) (-1.8977)
HHI -0.0284 0.1391*** 0.1347*** 0.1393*** 0.0702
(-0.5123) (3.7371) (3.2368) (3.7409) (1.3515)
INDSIZE 0.1061*** 0.0398*** 0.0425*** 0.0398*** 0.0541***
(6.4798) (5.1231) (5.1566) (5.1227) (5.1725)
NFIRMS -0.2011*** -0.1012*** -0.1048*** -0.1012*** -0.1324***
(-7.0272) (-8.2637) (-7.9029) (-8.2608) (-7.5215)
FCFIRM 0.2561** -0.0343 0.0229 -0.0335 0.0774
(2.5595) (-0.5604) (0.2952) (-0.5472) (0.6958)
MARGIN 0.2333*** 0.2377*** 0.2472*** 0.2377*** 0.2808***
(6.6555) (8.2641) (7.5753) (8.2641) (6.3765)
LEVDISP 1.8228*** 1.1270*** 1.1118*** 1.1271*** 1.0811***
(15.3788) (20.1912) (17.9101) (20.1920) (13.5927)
SIZEDISP 0.1373*** 0.0678*** 0.0667*** 0.0678*** 0.0785***
(5.2810) (4.5861) (4.0912) (4.5819) (3.8797)
ENTRYR 0.0735*** 0.0732*** 0.0573** 0.0732*** 0.0684***
(2.9277) (3.2806) (2.4976) (3.2805) (2.6353)
EXITR 0.0560* 0.0491* 0.0420 0.0492* -0.0326
(1.7687) (1.7444) (1.3206) (1.7474) (-0.8330)
--------------------------------------------------------------------------------------------
N 81567 81567 60078 81565 116882
r2_a 0.0646 0.1613 0.1548 0.1613 0.1592
--------------------------------------------------------------------------------------------
t statistics in parentheses
* p<0.1, ** p<0.05, *** p<0.013. 逐年 PSM和DID
逐年
**逐年匹配
use psmdata.dta, clear
*1:2卡尺最近邻匹配
*循环1:逐年进行PSM,并将各年份PSM结果保存,最后获得1998年至2007年共10年的匹配后数据集。
forvalue i = 1998/2007{
preserve //保留结果
capture {
*设置随机种子
keep if year == `i'
set seed 0000
gen norvar_2 = rnormal()
sort norvar_2
psmatch2 treated $xlist , outcome(TFPQD_OP) logit neighbor(2) ///
ties common ate caliper(0.05)
save `i'.dta, replace
}
restore
}
use 1998.dta, clear
*循环2:将各年份匹配后数据纵向合并至一个数据集中,生成我们回归需要的面板数据
forvalue k =1999/2007 {
capture {
append using `k'.dta
}
}
save ybydata.dta, replace //保存匹配后的面板数据和截面PSM相比,逐年PSM需要将逐年分开后一年年的匹配
- 循环 1 作用:逐年进行PSM,并将各年份PSM结果保存,最后获得1998年至2007年共10年的匹配后数据集。其中,preserve和restore方便高效使用数据,即不用在循环中写入
use psmdata.dta,clear。capture{ }是为了避免某些年份数据缺失导致Stata报错并停止运行,这里的年份都是连续的。- 循环 2 作用:将各年份匹配后数据纵向合并至一个数据集中,生成我们回归需要的面板数据。
- 平衡性检验
因为逐年PSM是一年年进行匹配的,所以我们要对比协变量的偏差,只能在同一年份内比较两组间是否存在系统性偏差,不同的年份的匹配的样本没有可比性。一般做法是:比较匹配前后不同年份 logit 回归结果,即如果匹配后各协变量的系数值减小、变得不显著和伪R方明显减小,则说明在不同年份两组的协变量不存在系统性偏差。
**逐年平衡性检验
*匹配前
forvalue i = 1998/2007 {
capture {
qui: logit treated $xlist i.ind3 if year == `i', vce(cluster prov)
est store ybyb`i'
}
}
local ybyblist "ybyb1998 ybyb1999 ybyb2000 ybyb2001 ybyb2002 ybyb2003 ybyb2004 ybyb2005 ybyb2006 ybyb2007"
esttab `ybyblist'
reg2docx `ybyblist' using 逐年平衡性检验结果_匹配前.docx, b(%6.4f) t(%6.4f) ///
scalars(N r2_p(%6.4f)) noconstant replace ///
indicate("Industry = *.ind3") ///
mtitles("1998b" "1999b" "2000b" "2001b" "2002b" ///
"2003b" "2004b" "2005b" "2006b" "2007b") ///
title("逐年平衡性检验_匹配前")
*匹配后
forvalue i = 1998/2007 {
capture {
qui: logit treated $xlist i.ind3 ///
if year == `i' & _weight != ., vce(cluster prov)
est store ybya`i'
}
}
local ybyblist "ybyb1998 ybyb1999 ybyb2000 ybyb2001 ybyb2002 ybyb2003 ybyb2004 ybyb2005 ybyb2006 ybyb2007"
esttab `ybyblist'
reg2docx `ybyalist' using 逐年平衡性检验结果_匹配后.docx, b(%6.4f) t(%6.4f) ///
scalars(N r2_p(%6.4f)) noconstant replace ///
indicate("Industry = *.ind3") ///
mtitles("1998a" "1999a" "2000a" "2001a" "2002a" ///
"2003a" "2004a" "2005a" "2006a" "2007a") ///
title("逐年平衡性检验_匹配后")平衡性检验的结果汇报
*匹配前的logit回归各个年份各个协变量的结果
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
1998b 1999b 2000b 2001b 2002b 2003b 2004b 2005b 2006b 2007b
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
treated
ADM 2.2684*** 2.3222*** 2.0865*** 1.9288** 1.4294* 2.0740** 2.0784* 1.5288 2.3137 2.7268**
(2.7355) (2.5959) (2.8096) (2.4781) (1.9008) (2.0923) (1.9458) (0.9822) (1.3856) (2.1562)
PPE -0.5244** -0.3025 -0.7743*** -0.5716** -0.7099*** -0.6272** -1.0487*** -1.0451*** -0.8431* -0.9608**
(-2.2990) (-1.5852) (-3.4052) (-2.3569) (-2.6279) (-2.2244) (-3.5397) (-2.7774) (-1.9164) (-2.1682)
ADV 0.0000 0.0000 0.0000 13.4355 0.0000 0.0000 26.4667** 34.6121** 31.8339** 16.2578
(.) (.) (.) (1.0514) (.) (.) (2.4702) (2.2337) (2.2127) (1.2177)
RD 0.0000 0.0000 0.0000 10.9171 0.0000 0.0000 0.0000 -1.3296 14.1701 8.3546
(.) (.) (.) (1.2536) (.) (.) (.) (-0.1238) (1.5283) (0.7065)
HHI -1.6439* -1.6918** -1.1028 -1.2699 -1.0869 -0.6338 0.0072 0.0714 -0.0496 0.0429
(-1.7219) (-1.9652) (-1.3282) (-1.4922) (-1.4629) (-0.8633) (0.0148) (0.1513) (-0.0896) (0.0784)
INDSIZE 0.5445* 0.4829* 0.3557 0.3033 0.2376 0.1528 -0.2555 -0.0907 -0.1805 -0.2358
(1.7667) (1.8760) (1.4057) (1.1672) (0.9226) (0.6146) (-1.2398) (-0.4178) (-0.7170) (-0.9694)
NFIRMS -0.3930 -0.2420 0.0200 0.1023 0.2644 0.3734 0.9632*** 0.6899** 0.7769** 0.8697**
(-0.6612) (-0.4746) (0.0427) (0.2083) (0.5603) (0.8035) (2.7205) (1.9736) (2.0972) (2.4071)
FCFIRM 1.6635 0.7963 1.6429 1.1912 0.7410 0.6982 2.0390** 0.8335 1.1705 1.5674*
(0.9054) (0.4392) (1.1530) (0.6450) (0.5633) (0.6334) (2.1761) (0.6433) (1.3389) (1.6736)
MARGIN 1.5995*** 1.4034*** 1.0741*** 1.2462*** 0.4034 0.8745** 1.2484** -0.3829 0.7840 0.1712
(3.5296) (3.5031) (2.8690) (3.1566) (0.8275) (2.0900) (2.3096) (-0.3499) (0.6127) (0.1870)
LEVDISP -0.9378 -0.8800 -1.3296 -1.3270 -0.9001 -1.1339 -0.9631 -1.2057 -1.6036 -1.5013
(-0.4328) (-0.5331) (-0.7892) (-0.7769) (-0.5507) (-0.6717) (-0.5041) (-0.6542) (-0.9766) (-0.9726)
SIZEDISP -0.0741 0.0517 0.0790 0.1699 0.1840 0.1689 0.5612*** 0.3714 0.5487** 0.6102**
(-0.2874) (0.2080) (0.3297) (0.7125) (0.6938) (0.7498) (2.7553) (1.4051) (2.1442) (2.1618)
ENTRYR 0.0000 -0.0619 0.9535* 0.2964 0.0387 0.0183 0.0348 -0.6241 -0.6629** -0.6837**
(.) (-0.1157) (1.7572) (0.5243) (0.1305) (0.0435) (0.1230) (-0.6853) (-2.1473) (-2.3081)
EXITR -0.9139 0.7341 0.0460 -0.5761 -0.3070 0.2523 0.8344** 0.0524 -0.5910 -0.5330
(-1.1158) (1.1616) (0.0659) (-0.8138) (-0.6607) (0.4841) (2.0014) (0.1361) (-0.9383) (-0.7851)
_cons -8.6621*** -8.8834*** -7.3079*** -6.6187** -5.6780** -5.4720** -2.9528 -2.3179 -2.4977 -1.5174
(-2.7961) (-3.3483) (-2.6862) (-2.2210) (-2.1561) (-2.1240) (-1.0200) (-0.8532) (-0.7556) (-0.4968)
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Industry Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes
N 6303 6600 6656 6845 7187 7601 9057 9428 10221 11207
r2_p 0.1321 0.1301 0.1337 0.1368 0.1369 0.1351 0.1578 0.1351 0.1314 0.1368
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
t statistics in parentheses
* p<0.1, ** p<0.05, *** p<0.01
*匹配后的logit回归各个年份各个协变量的结果
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
1998a 1999a 2000a 2001a 2002a 2003a 2004a 2005a 2006a 2007a
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
treated
ADM 0.8186 0.7099 1.0169 0.8462 0.1525 0.7434 0.0853 0.3600 0.8061 0.7568
(1.0061) (0.8124) (1.3867) (1.0619) (0.2048) (0.8235) (0.0714) (0.2385) (0.4899) (0.5814)
PPE 0.2349 0.3703* 0.1335 0.1864 0.2028 0.0637 -0.0651 -0.1128 -0.0983 -0.1607
(0.9089) (1.9154) (0.5660) (0.7556) (0.7784) (0.2231) (-0.2131) (-0.2964) (-0.2179) (-0.3868)
ADV 0.0000 0.0000 0.0000 6.5454 0.0000 0.0000 15.1587 4.7196 12.2655 -1.5428
(.) (.) (.) (0.6044) (.) (.) (1.3536) (0.2908) (0.8152) (-0.1188)
RD 0.0000 0.0000 0.0000 -8.3398 0.0000 0.0000 0.0000 -9.1278 -0.9288 -12.7757
(.) (.) (.) (-0.6978) (.) (.) (.) (-0.9596) (-0.0959) (-0.9324)
HHI -0.4786 -0.4828 -0.4323 -0.6529 -0.4950 -0.2469 -0.0630 -0.0505 0.2196 0.0863
(-0.5030) (-0.5685) (-0.5165) (-0.7708) (-0.6700) (-0.3173) (-0.1331) (-0.1042) (0.4048) (0.1496)
INDSIZE 0.2424 0.2039 0.0910 0.1361 0.1026 0.0569 -0.0786 0.0223 -0.0374 -0.1057
(0.7698) (0.8281) (0.3584) (0.5155) (0.3942) (0.2317) (-0.4091) (0.1061) (-0.1454) (-0.4386)
NFIRMS -0.1716 -0.0790 0.1095 0.0273 0.0924 0.1564 0.3901 0.2145 0.3206 0.4058
(-0.2827) (-0.1616) (0.2372) (0.0546) (0.1948) (0.3406) (1.1371) (0.6342) (0.8572) (1.1148)
FCFIRM 0.1643 -0.2306 -0.7050 -0.5302 -1.3960 -0.7499 -0.6088 -1.3333 -0.8095 -0.5513
(0.0941) (-0.1382) (-0.5092) (-0.3022) (-1.0856) (-0.7352) (-0.7719) (-1.0874) (-0.9200) (-0.6073)
MARGIN 1.1374** 0.7720* 0.7420* 0.5409 0.3343 0.4295 0.2948 -0.3597 0.3036 -0.0030
(2.3418) (1.7993) (1.9478) (1.2911) (0.6710) (1.0841) (0.5314) (-0.3368) (0.2356) (-0.0033)
LEVDISP -0.0022 0.2363 0.0725 0.5919 0.2944 0.4385 0.2644 0.2651 -0.0433 0.0963
(-0.0011) (0.1432) (0.0417) (0.3263) (0.1779) (0.2698) (0.1413) (0.1424) (-0.0264) (0.0619)
SIZEDISP -0.0387 0.0307 0.1642 0.1315 0.2040 0.2365 0.3054 0.1376 0.1875 0.2849
(-0.1369) (0.1286) (0.6774) (0.5625) (0.8189) (1.0679) (1.5141) (0.5676) (0.6690) (1.0209)
ENTRYR 0.0000 -0.0030 0.4019 0.0722 -0.2552 0.0391 -0.0099 -0.1736 -0.2510 -0.2626
(.) (-0.0054) (0.7407) (0.1290) (-0.8574) (0.0951) (-0.0325) (-0.2006) (-0.7387) (-0.9214)
EXITR -0.3475 0.1600 0.3100 -0.0141 -0.1314 0.2665 0.3176 0.1137 -0.0595 -0.1399
(-0.4376) (0.2422) (0.4429) (-0.0211) (-0.2864) (0.4944) (0.7820) (0.2809) (-0.0983) (-0.2001)
_cons -2.7021 -5.7169** -4.4212 -4.1241 -3.9158 -3.7323 -2.6553 -2.7141 -2.6220 -1.8506
(-0.9521) (-2.2631) (-1.6429) (-1.4217) (-1.4988) (-1.4734) (-0.9617) (-1.0106) (-0.7973) (-0.6046)
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Industry Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes
N 4576 4769 4813 4889 5168 5557 6418 6732 7387 8048
r2_p 0.0907 0.0934 0.0894 0.0931 0.0878 0.0917 0.0951 0.0836 0.0767 0.0797
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
t statistics in parentheses
* p<0.1, ** p<0.05, *** p<0.01从对匹配前和匹配后的各个年份各个协变量进行一一对比,可以看到大部分协变量在匹配后的 logit 回归参数都是不显著并且是变小了(少数几个协变量因为共线性而被omitted),而且所有回归的伪R方明显减小,这说明在不同年份两组的协变量不存在系统性偏差。
- 绘制倾向得分值的核密度图
sum _pscore if treated == 1, detail // 处理组的倾向得分均值为0.5698
*匹配前
sum _pscore if treated == 0, detail
twoway(kdensity _pscore if treated == 1, lpattern(solid) ///
lcolor(black) ///
lwidth(thin) ///
scheme(qleanmono) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", ///
size(medlarge) orientation(h)) ///
xtitle("{stSans:匹配前的倾向得分值}", ///
size(medlarge)) ///
xline(0.5698 , lpattern(solid) lcolor(black)) ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
saving(kensity_yby_before, replace)) ///
(kdensity _pscore if treated == 0, lpattern(dash)), ///
xlabel( , labsize(medlarge) format(%02.1f)) ///
ylabel(0(1)3, labsize(medlarge)) ///
legend(label(1 "{stSans:处理组}") ///
label(2 "{stSans:控制组}") ///
size(medlarge) position(1) symxsize(10))
*匹配后
sum _pscore if treated == 0 & _weight != ., detail
twoway(kdensity _pscore if treated == 1, lpattern(solid) ///
lcolor(black) ///
lwidth(thin) ///
scheme(qleanmono) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", ///
size(medlarge) orientation(h)) ///
xtitle("{stSans:匹配后的倾向得分值}", ///
size(medlarge)) ///
xline(0.5698 , lpattern(solid) lcolor(black)) ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
saving(kensity_yby_after, replace)) ///
(kdensity _pscore if treated == 0 & _weight != ., lpattern(dash)), ///
xlabel( , labsize(medlarge) format(%02.1f)) ///
ylabel(0(1)3, labsize(medlarge)) ///
legend(label(1 "{stSans:处理组}") ///
label(2 "{stSans:控制组}") ///
size(medlarge) position(1) symxsize(10))

匹配前后的和密度曲线和截面PSM类似,通过匹配前后的两条曲线可以发现,无论是匹配前后,处理组和控制组的得分偏差都比较大,但是在匹配后两组的均值距离缩短,两条曲线更加接近,因此一定程度上可以说明逐年匹配有效。
- 回归结果
**回归结果对比
use ybydata.dta, clear
*基准回归1(混合OLS)
qui: reg TFPQD_OP FB $xlist , cluster(city)
est store m1
*基准回归2(固定效应模型)
qui: reghdfe TFPQD_OP FB $xlist , $regopt
est store m2
*PSM-DID1(使用权重不为空的样本)
qui: reghdfe TFPQD_OP FB $xlist if _weight != ., $regopt
est store m6
*PSM-DID2(使用满足共同支撑假设的样本)
qui: reghdfe TFPQD_OP FB $xlist if _support == 1, $regopt
est store m7
*PSM-DID3(使用频数加权回归)
gen weight = _weight * 2
replace weight = 1 if treated == 1 & _weight != .
qui: reghdfe TFPQD_OP FB $xlist [fweight = weight], $regopt
est store m8
*回归结果输出
local mlist_2 "m1 m2 m6 m7 m8"
reg2docx `mlist_2' using 逐年匹配回归结果对比.docx, b(%6.4f) t(%6.4f) ///
scalars(N r2_a(%6.4f)) noconstant replace ///
mtitles("OLS" "FE" "Weight!=." "On_Support" "Weight_Reg") ///
title("基准回归及逐年PSM-DID结果")运行结果如下。回归结果与截面PSM - DID基本一致,因此也同样可以说明基准回归结果在考虑到选择偏差问题之后依然稳健。
--------------------------------------------------------------------------------------------
(1) (2) (3) (4) (5)
TFPQD_OP TFPQD_OP TFPQD_OP TFPQD_OP TFPQD_OP
--------------------------------------------------------------------------------------------
FB -0.124*** -0.0496*** -0.0493*** -0.0498*** -0.0466**
(-5.25) (-3.65) (-3.51) (-3.67) (-3.18)
ADM 1.068*** 0.872*** 0.892*** 0.871*** 0.912***
(17.64) (18.03) (15.33) (17.97) (11.45)
PPE -0.118*** -0.0845*** -0.0899*** -0.0848*** -0.114***
(-4.35) (-5.49) (-4.87) (-5.50) (-4.96)
ADV 3.424 0.403 0.389 0.377 4.492
(1.93) (0.25) (0.20) (0.24) (1.53)
RD -1.199 -3.512** -5.145** -3.539** -5.212*
(-0.81) (-2.66) (-2.93) (-2.66) (-2.12)
HHI -0.0284 0.139*** 0.151*** 0.139*** 0.0911
(-0.51) (3.74) (3.61) (3.73) (1.73)
INDSIZE 0.106*** 0.0398*** 0.0363*** 0.0397*** 0.0459***
(6.48) (5.12) (4.16) (5.10) (4.38)
NFIRMS -0.201*** -0.101*** -0.0975*** -0.101*** -0.120***
(-7.03) (-8.26) (-6.99) (-8.24) (-6.86)
FCFIRM 0.256* -0.0343 -0.104 -0.0388 0.0600
(2.56) (-0.56) (-1.33) (-0.63) (0.61)
MARGIN 0.233*** 0.238*** 0.224*** 0.237*** 0.308***
(6.66) (8.26) (6.83) (8.23) (7.20)
LEVDISP 1.823*** 1.127*** 1.165*** 1.127*** 1.159***
(15.38) (20.19) (18.21) (20.17) (14.10)
SIZEDISP 0.137*** 0.0678*** 0.0637*** 0.0678*** 0.0712***
(5.28) (4.59) (3.85) (4.58) (3.56)
ENTRYR 0.0735** 0.0732** 0.0635** 0.0743*** 0.0563*
(2.93) (3.28) (2.62) (3.32) (2.08)
EXITR 0.0560 0.0491 0.0468 0.0483 0.0201
(1.77) (1.74) (1.45) (1.71) (0.48)
_cons 0.583***
(4.00)
--------------------------------------------------------------------------------------------
N 81567 81567 58926 81507 116269
--------------------------------------------------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001