Chapter7——STATA矩阵
Chapter7——STATA矩阵
STATA在9.0版本更新了矩阵组件,出现了与其他专门的矩阵运算软件功能一 样强大的新组件 MATA,用 MATA 可以完成除绘图以外的所有STATA数据处理和分析功能。以下是传统的STATA矩阵命令的教程。
0. 生成矩阵
- 输入新矩阵
matrix A=(1,0,1\2,1,0\-3,2,-5) //手动录入矩阵A
matrix list A //显示录入的矩阵A
matlist A //显示录入的矩阵A
matrix B=(1+2,2*3/4\5/2,3^2)
matrix list B
matrix C=(2,3,4) //只有一行的矩阵
matrix E=(1\2\3) //只有一列的矩阵
matrix F=(4) //只有一个数字的矩阵
matrix rownames A = sex edu marriage
matrix colnames A =obs1 obs2 obs3
matrix list
/* rownames是生成行名字,colnames是生成列名字
| obs1 obs2 obs3
-------------+---------------------------------
sex | 1 0 1
edu | 2 1 0
marriage | -3 2 -5 */- 生成特定格式矩阵
*生成一个5行3列的矩阵A,矩阵中的元素均为0
matrix A=J(5,3,0)
*生成一个6阶单位阵I,只有对角位置值为1
matrix I=I(6)
/*symmetric I[6,6]
c1 c2 c3 c4 c5 c6
r1 1
r2 0 1
r3 0 0 1
r4 0 0 0 1
r5 0 0 0 0 1
r6 0 0 0 0 0 1*/
*生成一个 3 行 5 列的随机矩阵 R,每个随机元素均服从(0,1)均匀分布
matrix R=matuniform(3,5)
/*R[3,5]
c1 c2 c3 c4 c5
r1 .3488717 .26688571 .13664629 .02855687 .86893327
r2 .3508549 .07110509 .32336795 .55510316 .87599101
r3 .20470947 .89275869 .5844658 .36977914 .85063091*/
*以d中的元素为对角元素生成对角矩阵D
matrix d=(1,4,9)
matrix D=diag(d)
matrix list D
/*symmetric D[3,3]
c1 c2 c3
c1 1
c2 0 4
c3 0 0 9*/- 数据与矩阵之间的互相转化
*Create matrix from variables
mkmat varlist [if exp][in exp][matrix (matname) nomissing]
*Create variables from matrix
svmat [type] A [, names(col|eqcol|matcol|string)]- 数据转化成矩阵
sysuse auto,clear
*将 foreign weight displ 这三个变量的前5个观察数据转换为矩阵X
mkmat foreign weight displ in 1/5,matrix(X)
matrix list X
/*X[5,3]
foreign weight displacement
r1 0 2930 121
r2 0 3350 258
r3 0 2640 121
r4 0 3250 196
r5 0 4080 350*/
*将带条件的数据转换为矩阵 Y,条件是fore==1的这三个变量转化成矩阵输出
mkmat foreign weight displ if foreign==1,matrix(Y)
matrix list Y- 矩阵转换成数据
matrix A=(1,0,1\2,1,0\-3,2,-5)
svmat A //将矩阵 A 中的数据转化为数据,变量为 A1,A2,A3
list
svmat A,name(ccb) //将矩阵 A 中的数据转化为新的变量 ccb1,ccb2,ccb31. 矩阵的四则运算
| 运算 | STATA命令 | 说明 |
|---|---|---|
| C=A±B | mat c = a±b | dim(a)=dim(b) |
| C=A*B | mat c =a*b | cols(a)=rows(b') |
| C=A-1 | mat c = inv(b) | b为方阵,求b的逆矩阵 |
| C=A/k | mat c =a/k | k为常数 |
| C=A×B | mat c = a#b | 直乘运算 |
- 矩阵扩展
*相同行数的矩阵之间左右相加和并
matrix A=(1,0,1\2,1,0\-3,2,-5)
matrix B=(4\3\7)
matrix C=(A,B) //在矩阵A右边加单列矩阵B
matrix list C
/*C[3,4]
c1 c2 c3 c1
r1 1 0 1 4
r2 2 1 0 3
r3 -3 2 -5 7*/
*列数相同的矩阵之间上下相加合并
matrix D=(10,9,25)
matrix E=(A\D) //在矩阵A下面再加一行
matrix list E
/*E[4,3]
c1 c2 c3
r1 1 0 1
r2 2 1 0
r3 -3 2 -5
r1 10 9 25*/- 矩阵的加、减、数乘、除法
*矩阵相加
mat e=(3,5\2,0)
mat t=(1,3\2,1)
/*t[2,2] e[2,2]
c1 c2 c1 c2
r1 1 3 r1 3 5
r2 2 1 r2 2 0*/
mat r1=e+t //本质:(3+1,5+3\2+2,0+1)
mat list r1
*矩阵相减
mat r2=e-t //本质:(3-1,5-3\2-2,0-1)
mat list r2
*矩阵标量数乘
mat e2=e*2 //每个元素均乘标量2,本质:(3*2,5*2\2*2,0*2)
mat list e2
*矩阵标量除法
mat e3=e/10 //每个元素均除以标量10
mat list e3- 矩阵乘法、直乘及Kronecker乘积运算
*矩阵间相乘
mat w=e*t
mat list w
*矩阵乘法不满足交换律,一般来说 a*b不等于b*a
mat a=(2,3\1,-2\3,1)
mat b=(1,-2,-3\2,-1,0)
mat ab=a*b
mat list ab
mat ba=b*a
mat list ba
*两个矩阵对应元素直接相乘,要求两个矩阵结构相同
mat A=(1,2\3,4\5,6)
mat B=(7,8\9,0\1,9)
matrix H=hadamard(A,B) //要求矩阵A和矩阵B的size是一样的,一一对应相乘
mat list H //其实就是两个规格一样的矩阵一一对应相乘
/* c1 c2
r1 7 16
r2 27 0
r3 5 54*/- Kronecker乘积运算对A和B没有size的任何,要求矩阵的 Kronecker乘积:
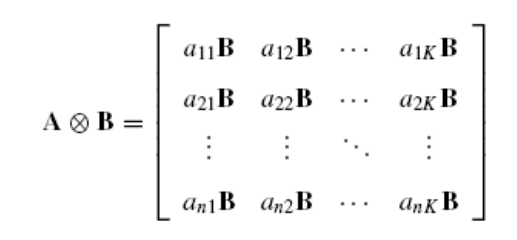
mat ab2=a#b
mat list ab2
/*ab2[6,6]
c1: c1: c1: c2: c2: c2:
c1 c2 c3 c1 c2 c3
r1:r1 2 -4 -6 3 -6 -9
r1:r2 4 -2 0 6 -3 0
r2:r1 1 -2 -3 -2 4 6
r2:r2 2 -1 0 -4 2 0
r3:r1 3 -6 -9 1 -2 -3
r3:r2 6 -3 0 2 -1 0*/
-------------------------------------------------------------------------------------
mat ba2=b#a
mat list ba2
/*ba2[6,6]
c1: c1: c2: c2: c3: c3:
c1 c2 c1 c2 c1 c2
r1:r1 2 3 -4 -6 -6 -9
r1:r2 1 -2 -2 4 -3 6
r1:r3 3 1 -6 -2 -9 -3
r2:r1 4 6 -2 -3 0 0
r2:r2 2 -4 -1 2 0 0
r2:r3 6 2 -3 -1 0 0*/2. 矩阵函数
| 函数名称 | 说明 |
|---|---|
| cholesky(B) | 裘氏分解,返回P,使PP‘=B-1,B为对称、正定矩阵 |
| corr(B) | |
| diag(V) | 若V为1×n或n×1,则返回对角元素为V的n×n矩阵 |
| get(name) | return system matrix (see help get()) |
| hadamard(A,B) | 返回矩阵C,满足C[i,j]=A[i,j]*B[i,j] |
| I(n) | 返回n×n单位矩阵 |
| inv(B) | 返回方阵B的逆矩阵B-1 |
| J(r,c,z) | 返回r×c矩阵,矩阵中的所有元素都是常数z |
| matuniform(r,c) | |
| nullmat(A) | 对于mat c =(nullmat(a),b)。若a不存在,c=b;否则,c=(a,b) |
| sweep(A,z) | sweep of square matrix;return A with zth row/column swept |
| syminv(B) | inverse of symmetric matrix;if B is not positive definite |
| vec(A) | 将矩阵A向量化后返回B,及所有列一次堆积 比如:Am×n,则Bmn×1 |
| vecdiag(B) | 返回一个行向量,包含方阵B的对角元素 |
| 函数名称 | 返回值说明 |
| colnumb(A,s) | 返回矩阵A中的第一个名称为字符串s的所在的列数 |
| colsof(B) | 返回矩阵B的列数 |
| det(B) | 返回矩阵B的行列式 |
| diag0cnt(B) | 返回矩阵B中对角线为零的元素的个数 |
| el(A,i,j) | 返回矩阵A中第[i,j]个元素,等价于A[i,j] |
| issym(A) | 判断矩阵A中是否为对称矩阵,是返回1,否返回0 |
| matmissing(A) | 判断矩阵A中是否含有缺漏项,是返回1,否返回0 |
| mreldif(B,C) | 返回矩阵B和C的相对差异 |
| rownumb(A,s) | 返回矩阵A中第一个名称为字符串s的行所在的行数 |
| rowsof(B) | 返回矩阵B的行数 |
| trace(B) | 返回方阵B的秩 |
- 装置、求迹
mat b=(1,-2,-3\2,-1,0)
mat list b
mat b2=b' //b2为b的转置矩阵
mat list b2
*如果是"数据集"中的数据进行行列互换转置,可以用过xpose命令来实现,注意和矩阵转置区分
use math,clear
xpose,clear- 求逆矩阵、求行列式的值
*=======求逆矩阵=======
matrix B=inv(A) //B 为 A 的逆矩阵
mat list B
*任务:解线性方程 Ax=b,其中:A=(1,-1,1,-2\2,0,-1,4\3,2,1,0\-1,2,-1,2) b=(2\4\-1\-4)
mat A=(1,-1,1,-2\2,0,-1,4\3,2,1,0\-1,2,-1,2)
mat b=(2\4\-1\-4)
*生成A的逆矩阵a=A-1,然后得x=a*b
matrix a=inv(A)
mat x=a*b
mat list x
*=======求行列式========
mat a=(1,0,1\2,1,0\-3,2,-5)
mat aa1=det(a) //计算矩阵a的行列式,并且把该结果放到矩阵aa1中
display aa1
scalar aa2=det(a) //计算矩阵a的行列式,并且把该结果以标量形式存储
mat list aa2
mat d=(1,-1,1,-2,2\2,0,-1,4,4\3,2,1,0,-1\-1,2,-1,2,-4)
mat dd=det(d)
scalar list- 返回或者修改矩阵中的某个元素的值
el(A,i,j)=A[i,j]
*syntax:el(A,i,j)=A[i,j] 两种方法来索引返回矩阵中的某行某列的某个元素
*example:
mat d=(1,-1,1,-2,2\2,100,-1,4,4\3,2,1,0,-1\-1,2,-1,2,-4)
scalar dd=d[2,2] //函数1:返回第2行第2列的矩阵d元素
scalar ddd=el(d,2,2) //函数2:返回第2行第2列的矩阵d元素
scalar list
mat d[1,3]=1000 //把矩阵d的第一行第三列的数字修改成1000
mat list d- Nullmat命令
nullmat在矩阵中的函数运算有点像数据管理中的merge,可以实现两个矩阵的横向对接
mat A=I(3)
mat B=J(3,3,9)
mat list C //matrix C not found
mat C=(nullmat(C),A) //当C矩阵不存在时,将得到C=A
mat list C //C=A
mat C=(nullmat(B),A) //C变成由B和A两个矩阵横向对接
mat list C //C=(B,A)
mat A=A/10
mat C=(nullmat(C),A) //C在原来的基础上对接了A变成新的矩阵
mat list C //C=(C,A- 其他矩阵函数
*将矩阵转换为一维列矩阵
matrix A= (1,0,1\2,1,0\-3,2,-5)
mat e=vec(A) //将矩阵A转化为一维列矩阵e
mat list e
*索引返回某个矩阵中的对角元素生成以该对角元素的一行向量
mat d=vecdiag(A) //返回矩阵A的对角元素为一行向量d
mat list d
mat J=J(10,2,.) //生成10×2的空白矩阵,矩阵内的元素全是.
scalar a=rowsof(J) //生成矩阵J的行数的标量值a
scalar b=colsof(J) //生成矩阵J的列数的标量值的d
scalar list
/* b = 2
a = 10*/