图论最短路径——Dijkstra算法

图论最短路径——Dijkstra算法

1. 图的基本概念

图论中的图（Graph）是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

一个图可以用数学语言描述为G(V(G),E(G))。V(vertex)指的是图的顶点集，E(edge)指的是图的边集。

根据边是否有方向，可将图分为有向图和无向图。另外，有些图的边上还可能有权值，这样的图称为有权图。

image-20220811144122296

（online graph）Graph Editor (csacademy.com)

  1. 无向图的权重邻接矩阵

图上的每一个节点之间都是没有相互方向的关系，但是每一条边都存在一定的距离权重

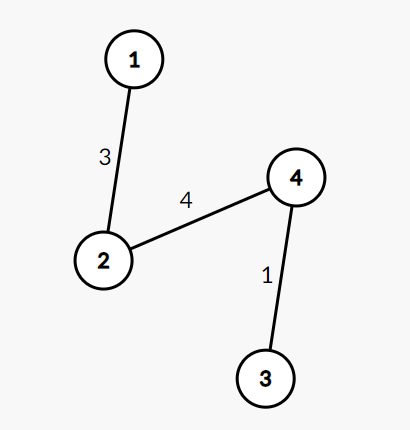
image-20220811144333524

  • 矩阵图：

  • 结论：

  1. 无向图对应的权重邻接矩阵D是一个对称矩阵
  2. 其矩阵是对称矩阵，期对角线上元素为0
  3. Dij表示的是第i个节点到第j个节点的权重
  1. 有向图的权重邻接矩阵

图上的每一个节点之间都是存在之间相互方向的关系，同时每一条边都存在一定关于表示距离的权重

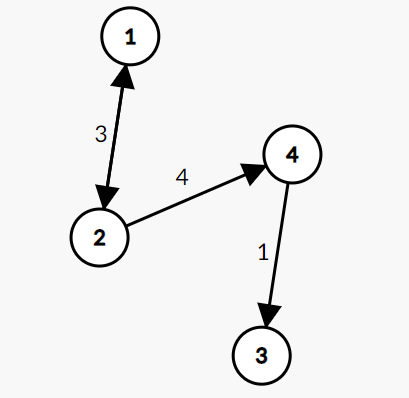
image-20220811150018777

  • 矩阵图

  • 结论：
  1. 有向图对应的权重邻接矩阵D是一般不再是对称矩阵
  2. 其主对角线上元素为0
  3. Dij表示第i个节点到第j个节点的权重
2. Dijkstra(迪杰斯特拉)算法

Dijkstra 算法是典型最短路算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

  • 算法描述：

  1. 初始化集合 E ，使之只包含源节点 S ，并初始化集合 R，使之包含所有其它节点。初始化路径列O ，使其包含一段从 S 起始的路径。这些路径的长度值等于相应链路的量度值，并以递增顺序排列列表O ；

  2. 若列表O 为空，或者O 中第 1 个路径长度为无穷大，则将 R中所有剩余节点标注为不可达，并终止算法；

  3. 首先寻找列表O 中的最短路径 P，从O 中删除 P。设V 为 P的最终节点。若V 已在集合 E 中，继续执行步骤 2。否则， P为通往V 的最短路径。将V 从 R移至 E ；

  4. 建立一个与 P相连并从V 开始的所有链路构成的侯选路径集合。这些路径的长度是 P的长度加上与 P相连的长度。将这些新的链路插入有序表O 中，并放置在其长度所对应的等级上。继续执行步骤 2

  • 步骤演示：

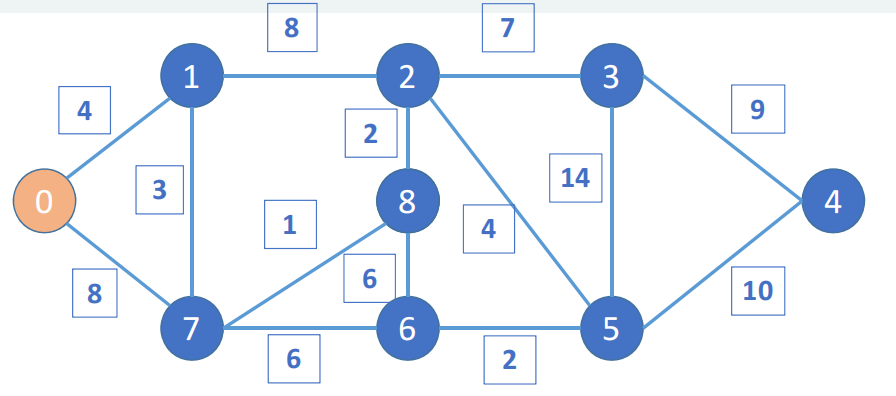
以一个节点作为中心寻找能够找得到的节点作为目标路径，且存在多个目标路径，比如是从0到7的路径有0-1-7和0-7，前者的距离要短于后者

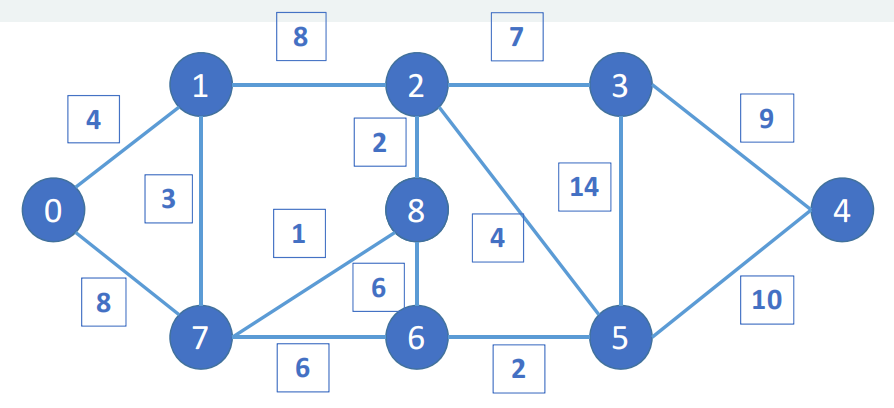
设置开始节点为1，结束节点为4，寻找从1到4的最短距离，其中节点之间的权重代表的是节点间的距离

image-20220811150948717

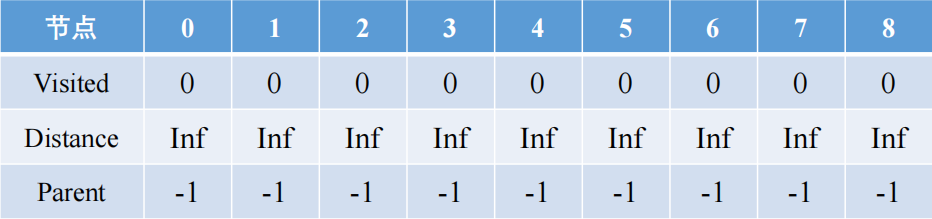
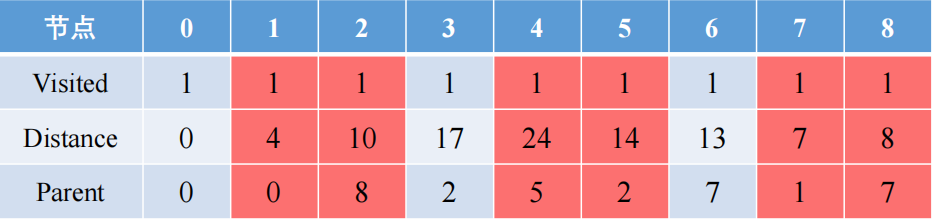
visited 表示该节点是否有被访问到，即是在遍历的所有路径中的最短的路才会被访问

distance 表示从起始节点到该节点的距离加和

parent 表示上一个父亲节点是哪个节点，即是这个位置对应的上一个位置是哪里

image-20220811151126938

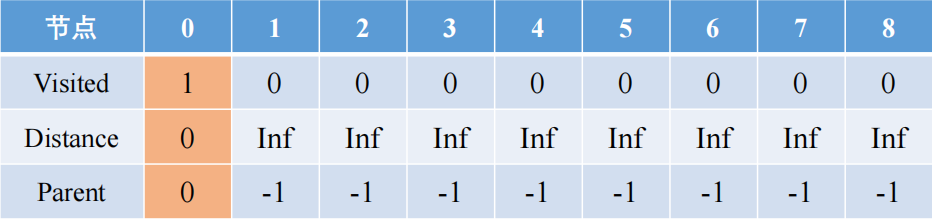
从0开始，找到0最近的节点是1和7

image-20220811151627093

image-20220811230237998

image-20220811151739348

在0这个位置到1的距离是2，到7的距离是8，同时4和8都是小于inf的，所以这两条路是可行的，但是0-1的距离是最短的，所以选择访问1，且1和7的父亲节点都是0

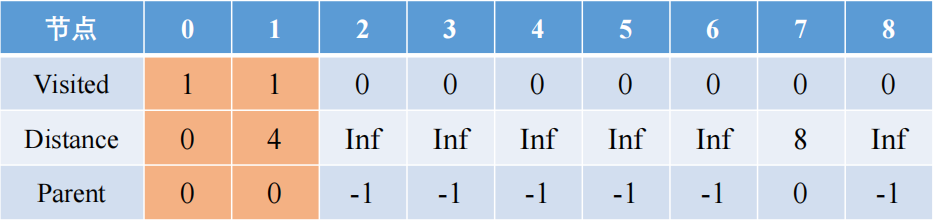
image-20220811152144682

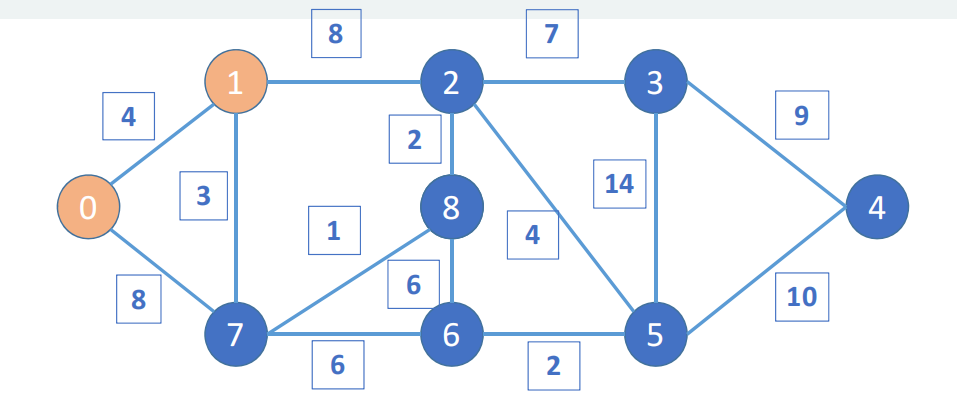
image-20220811213056094

image-20220811152504266

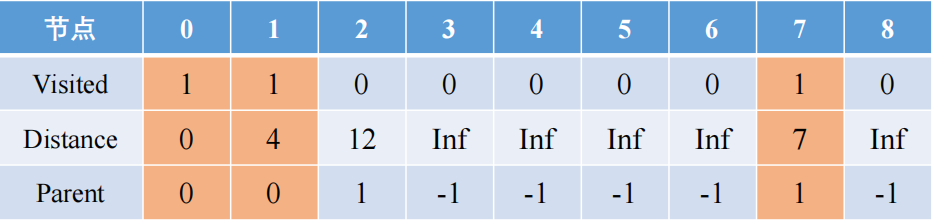
从1被访问后更新为新的出发点，从1出发，可以去2和7，距离分别是8和3，更新后从0-1-2和0-1-7的距离分别是12和7，后者距离更短，所以7被访问

image-20220811152726262

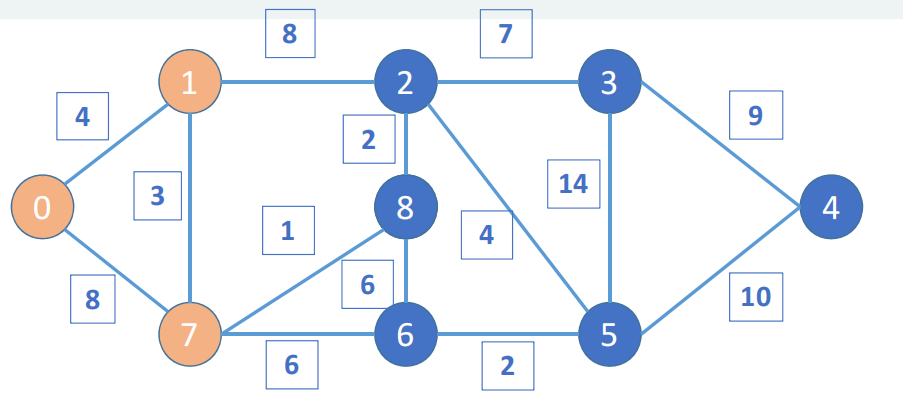
image-20220811154203936

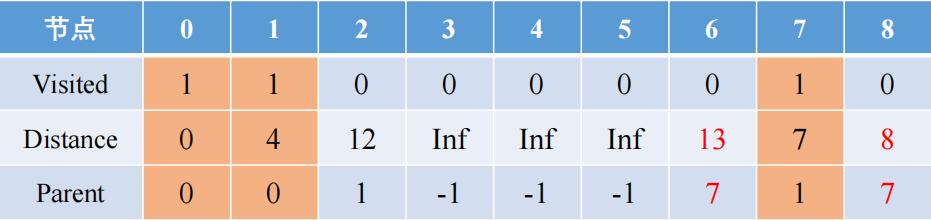
image-20220811154552891

从7出发，有8和6节点，距离分别是1和6，更新后的路径有0-1-7-8和0-1-7-6，其距离分别是8和13，前者距离更短，所以8被访问了

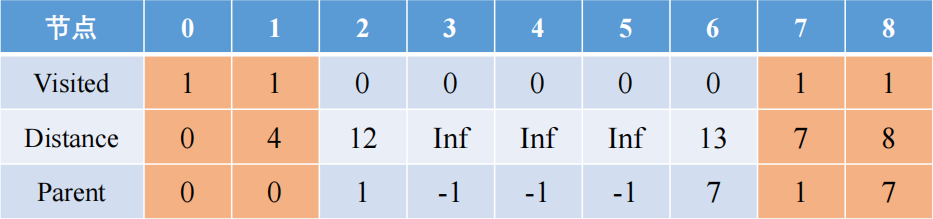
image-20220811154705824

image-20220811154726287

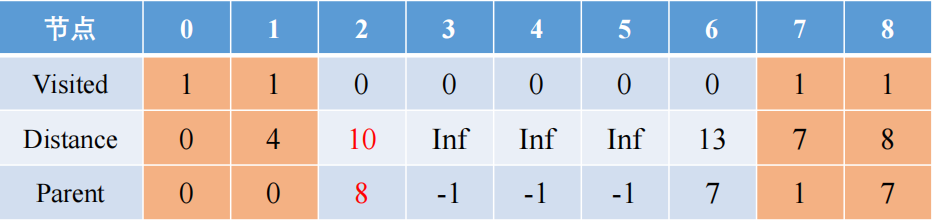
image-20220811155424709

从8出发，有2和6两个节点选择，其距离分别是2和8，更新后的路径有0-1-7-8-2和0-1-7-8-6，前者距离是10小于此前遍历到2的距离12，后者的距离是14大于此前遍历到6的距离13，所以前者的路径短于后者，节点2被访问

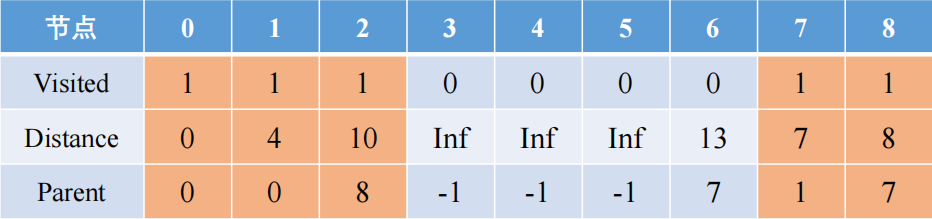
image-20220811155706370

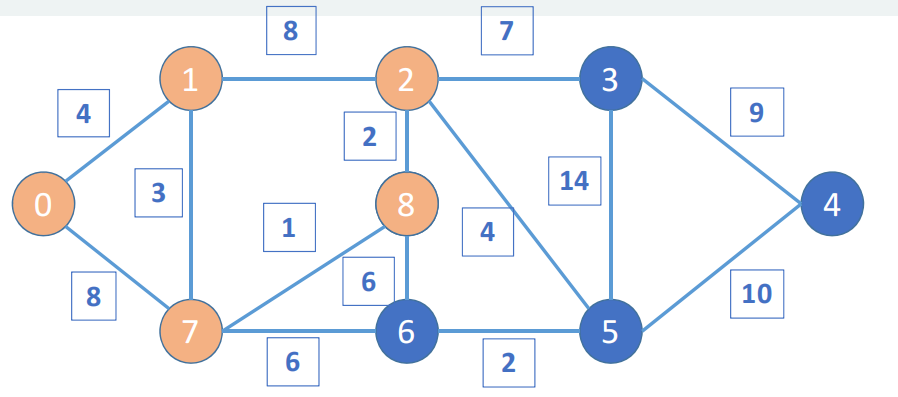
image-20220811155612918

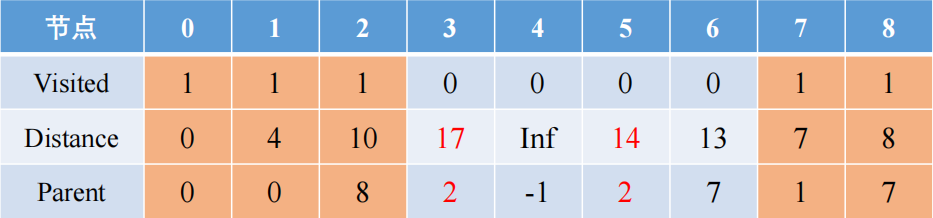
image-20220811155918796

从2出发的附近节点有5和3，其距离是4和7，更新后的整体路径有0-1-7-8-2-3和0-1-7-8-2-5，前者的距离是17大于后者的距离是14，所以后者节点5被路径访问

image-20220811155948701

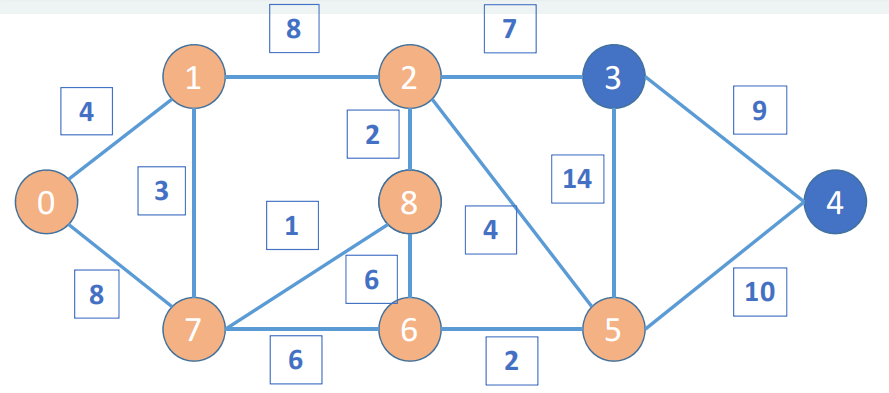
image-20220811160010406

从节点5出发，附近路径的节点有3和4，其距离是14和10，更新后的整体路径是0-1-7-8-2-5-3和0-1-7-8-2-5-4，前者的距离是28大于此前遍历过的路径距离17，同时也大于后者的距离24，所以4被访问

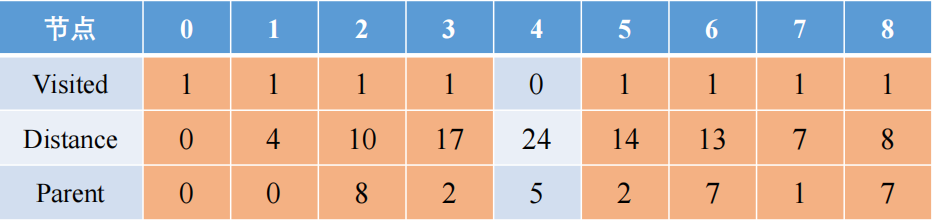
image-20220811160302563

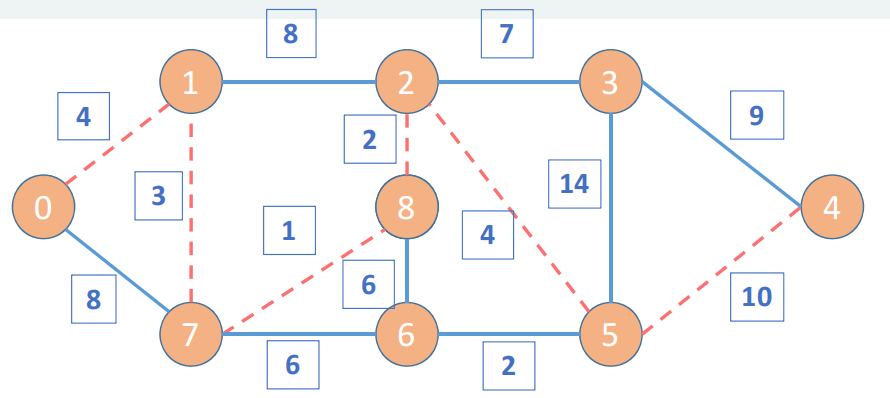
最终从起点0和重点4都被访问了，最短路径的选择结束，最短的路径是0-1-7-8-2-5-4，其路径距离是24，可以通过父亲节点寻找得出最短路径的结论

image-20220811160514862

image-20220811160530475

3. Dijkstra算法代码实现
% 生成上述的节点图(因为matlab的编号从1考试，所以以9表示为数字0)
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4]
t = [1 7 7 2 8 5 3 6 8 8 5 3 4 3]
w = [4 8 3 8 2 4 7 6 2 6 2 14 10 9]  % 生成图中的节点权重
G = graph(s,t,w)
plot(G,'EdgeLabel',G.Edges.Weight, 'linewidth', 2) % 标记权重Edgelabel，'linewidth'设置线宽度
set( gca, 'XTick', [], 'YTick', [] )   % 在画图后不显示坐标
[P,d] = shortestpath(G, 9, 4)  % 从9出发到4的最短路径,p是路径,d是距离
% outcome:
% P =
     9     1     7     8     2     5     4
% d =
    25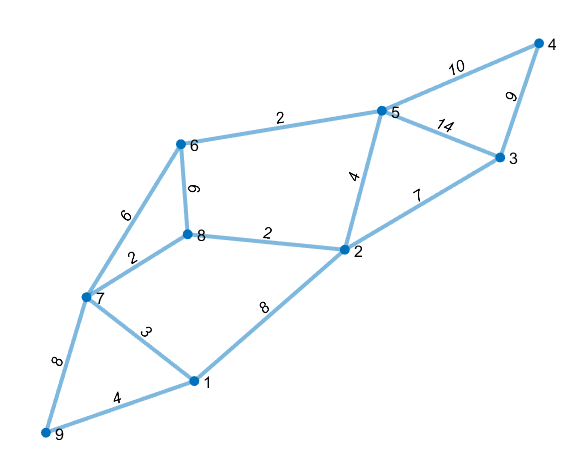

image-20220811221636122

% 在图中高亮我们的最短路径
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
highlight(myplot, P, 'EdgeColor', 'r')
% 求出任意两点的最短路径矩阵
D = distances(G)

image-20220811221820379

% 返回图形 G 中与节点 s 的距离在 d 之内的所有节点
[nodeIDs,dist] = nearest(G, 2, 10)
% outcome：
% nodeIDs =
     8
     5
     7
     6
     1
     3
% dist =
     2
     4
     4
     6
     7
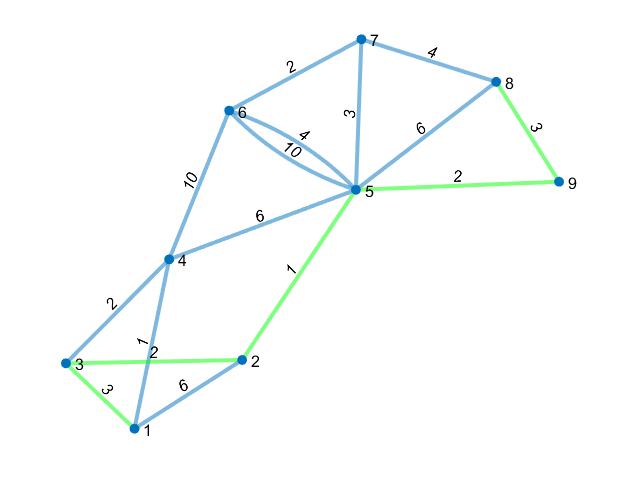
     7
4. Dijkstra案例

image-20220811223839256

s = [1 1 1 2 3 3 4 5 5 5 5 6 6 7 9 9]
t = [2 4 3 5 2 4 6 4 6 7 8 7 5 8 8 5]
w = [6 1 3 1 2 2 10 6 4 3 6 2 10 4 3 2]
G = graph(s,t,w)
plot(G,'EdgeLabel',G.Edges.Weight, 'linewidth', 2)
set( gca, 'XTick', [], 'YTick', [] )
[P,d] = shortestpath(G, 1, 8) 
% outcome:
% P =
     1     3     2     5     9     8
% d =
     11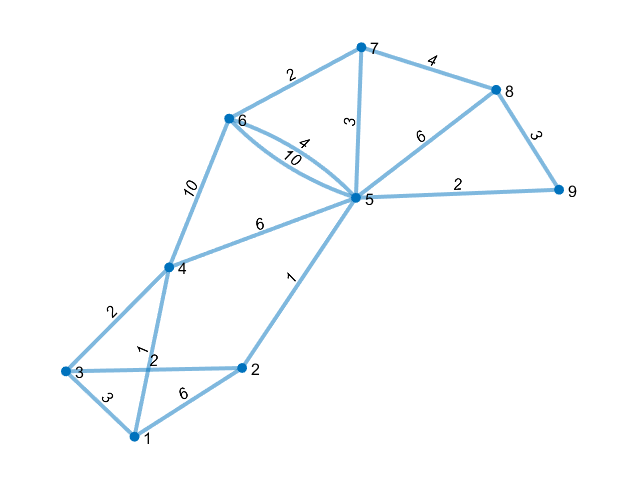

image-20220811224605328

myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
highlight(myplot, P, 'EdgeColor', 'g')

image-20220811225508934