双重差分模型1
双重差分假设和基准回归
1. DID介绍
中文名“双重差分法”,英文名“Differences-in-Differences”,别名“倍差法”,小名“差中差”,双重差分法估计的本质简单理解其实就是面板数据固定效应估计,近年来由于DID具有良好的一些性质,很多人的使用于政策效应的评估。
使用DID的理由:
- 可以很大程度上避免内生性问题的困扰
- 传统方法下评估政策效应,主要是通过设置一个政策发生与否的虚拟变量然后进行回归,相较而言,双重差分法的模型设置更加科学,能更加准确地估计出政策效应
- 双重差分法的原理和模型设置很简单,容易理解和运用,并不像空间计量、DSGE等方法一样让人望而生畏
2. 基准模型设定
- DID模型实现的前提条件是:
- 跨度至少是两年的面板数据
- 政策冲击并非一刀切,具有受政策影响的实验组和不受政策影响的对照组
- DID的基准模型设定,如下所示
其中,du为分组虚拟变量,若个体 i 受政策实施的影响,则个体 i 属于处理组(treated),对应的du取值为1,若个体 i 不受政策实施的影响,则个体 i 属于对照组,对应的du取值为0。dt为政策实施虚拟变量(post),政策实施之前dt取值为0,政策实施之后dt取值为1。du×dt为分组虚拟变量与政策实施虚拟变量的交互项,其系数就反映了政策实施净效应,也是我们使用DID时最为关注的系数。
再看DID的两个模型的前提假设,如果没有时间跨度两年的面板数据,就无法分出政策实施虚拟变量,若政策冲击是一刀切的,则无法找到于此对应合适的对照组,即是无法分组。
- 关于交互项的参数
| 政策实施前 | 政策实施后 | Difference | |
|---|---|---|---|
| 处理组 | α0+α1 | α0+α1+α2+α3 | α0+α1 |
| 对照组 | α0 | α0+α2 | α2 |
| Difference | α1 | α0+α3~ | α3(D-in-D) |
很显然,是两次差分的结果,一次差分在时间维度,一次差分在个体维度。更直观地,可以用图形来表述上图以及DID的逻辑:
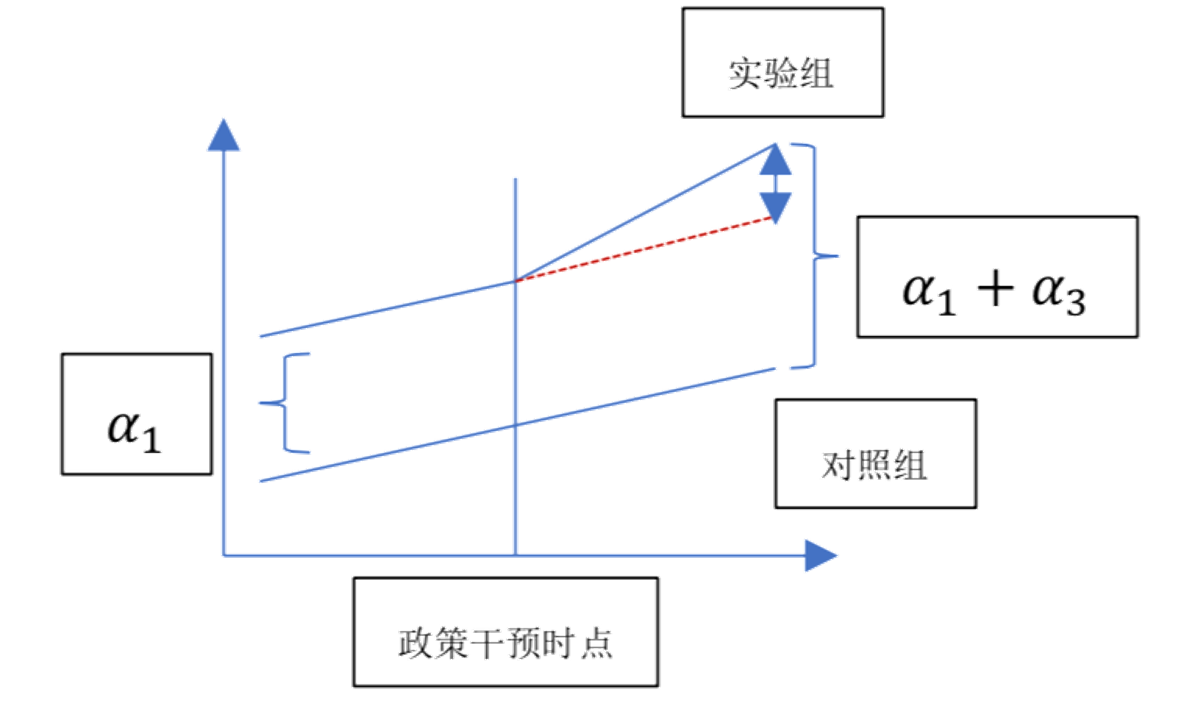
图中红色虚线表示的是假设在没有政策干扰的情况下,实验组的变化趋势,即实验组的反事实情况。实际上,这个图形也反映出了DID最为重要和关键的前提条件:平行趋势(Common Trends),也就是说,处理组和对照组在政策实施之前必须具有相同的变化趋势,即是在政策实施之前两者变化是不存在显著的差异的。
举个增高药的例子: 小明购买了一个增高药想要增高,想知道该增高药对增高是否存在显著的作用,于是他对增高药的效果做了DID,他找来了小高,小高在过去十年的时间里面身高增长的高度和小明增长的高度是一致的,即是二者的身高变化是服从平行趋势的,基于历史会重演的假设,我们可以认为小高可以作为小明的反事实对照组,就是小明假如没有吃增高药,他的身高变化应该是多少。当小明吃下增高药1年后发现增高了3厘米,小高仅增高了1厘米,此时可以认为1厘米是小明没有吃增高药的情况下所增长的身高,而二者相差的2厘米是增高药的作用,即是政策的效应。
因此,总结来说,双重差分法的基本思想或原理就是通过对政策实施前后对照组和处理组之间差异的比较构造出反映政策效果的双重差分统计量。将该思想与上表的内容转化为简单的模型,这个时候只需要关注模型中交互项的系数,就得到了想要的DID下的政策净效应。上述模型是DID的基准形式,在实际使用时,只需要加上控制变量就可以了。